2017-10-25
562
Прямая в R2.
Допустим, дана точка 
с координатами 
и перпендикуляр (синоним: «нормаль») к прямой, вектор 
. Если произвольную точку 
с координатами 
взять вне этой прямой, то 
и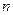 
не перпендикулярны, а если принадлежит прямой, то перпендикулярны, тогда их скалярное произведение 0.
На чертеже 
. Вектор = 
(из координат конца вектора вычли координаты его начала).
Тогда 
, откуда 
, обозначим 
через С, и получим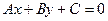 
.
Таким образом, мы заодно ещё и доказали, что координаты нормали являются коэффициентами при x,y в уравнении прямой.
Замечание. От длины нормали уравнение не зависит. Если вектор нормали умножить на 
, то все коэффициенты уравнения, включая константу, будут больше в раз, но тогда можно вынести число и сократить на него всё уравнение, а справа 0 так и останется 0. То есть, получим уравнение той же самой прямой, и от длины нормали ничего не зависит.
Плоскость в R3.
Уравнение плоскости по точке и перпендикуляру. Абсолютно аналогичная технология вывода уравнения применяется и для плоскости. Пусть дана точка с координатами 
и перпендикуляр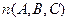 
. Сейчас мы докажем, что именно эти координаты А,В,С окажутся коэффициентами в уравнении плоскости. Рассмотрим произвольную точку 
, принадлежащую плоскости. Тогда вектор перпендикулярен нормали, то есть вектору .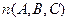
Тогда скалярное произведение, пары векторов 
и 
равно 0. Итак, 
. Раскроем скобки: 
.
Обозначим константу 
. Тогда получается 
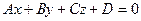. Обратите внимание, что координаты нормали оказались именно коэффициентами при x,y,z.
Пример. Найти уравнение плоскости, проходящей через точку (1,1,1) перпендикулярно вектору (1,2,3).
Решение. Вектор 
ортогонален вектору (1,2,3).
Тогда 
следовательно,
.
Замечание. Длина нормали не влияет на уравнение. Если бы изначально было дано, что нормаль (2,4,6) то получили бы:
, но это уравнение задаёт ту же самую плоскость. Достаточно вынести 2 за скобку, и сократить на 2, получили бы 
.
