2017-10-25
569
Сначала выведем формулу проекции вектора на ось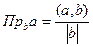 
.
(чертёж с доски)
1) длина проекции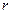 
это катет, 
гипотенуза треугольника, тогда получается, что 
.
2) известно, что 
.
Сопоставим эти 2 факта. 
, тогда 
, откуда и следует 
.
Пусть теперь дана прямая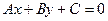 
и точка 
. Кратчайшее расстояние, то есть длину перпендикуляра, проведённого от точки к прямой, обозначим d. Нам не известно, где основание перпендикуляра, более того, его и не нужно искать. Возьмём произвольную точку 
на прямой. Это можно сделать так: присвоим x=0 и вычислим y, либо наоборот, y=0 и вычислить x. Короче, найти какую-нибудь точку на прямой можно элементарно. Далее, соединим и 
. Вектор 
не перпендикулярен прямой, однако его проекция на нормаль это и есть d.
Применим формулу проекции вектора на ось. 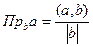. В нашем случае это 
. Но расстояние всегда положительно, независимо от того, с какой стороны от прямой эта точка. Поэтому в числителе должен быть ещё и модуль, а не само скалярное произведение.
, если расписать это подробнее, то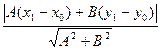 
т.е. 
.
Замечание. Если точка принадлежит прямой, то в числителе 0, и тогда d = 0, что и должно получиться, ведь точка лежит на прямой.
Пример. Найти расстояние от точки M1(2,1) до прямой 
.
Решение. Нормаль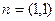 
. Тогда 
= 
.
