Пункт 2. Вывод уравнений по точке и направляющим векторам

Прямая в R². Пусть задана точка с координатами и направляющий вектор 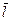с координатами 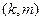. Поставим произвольную точку на прямой. В данном пункте не ортогонален, а коллинеарен вектору 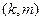, то есть координаты векторов и 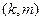пропорциональны.

Запишем пропорцию: 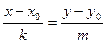Это называется «каноническое уравнение прямой». Можно свести к общему виду, умножив крайние и средние члены пропорции:

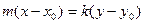, сводится к .

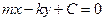Заметим, что здесь 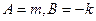. То есть, можно было бы и сразу от направляющего перейти к нормали, для этого поменять местами координаты вектора, и у одной координаты сменть знак. А потом действовать как в прошлом пункте.

Пример. Найти уравнение прямой, проходящей через точку (1,2) параллельно вектору (3,4).

Решение. , , .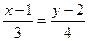

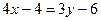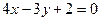Замечание. Построение уравнения прямой по двум точкам сводится к этому же методу, так как вектор, проведённый между этими точками, как раз и есть направляющий к прямой.

Плоскость в R³. Для плоскости, необходимо 2 направляющих. Пусть даны точка и 2 направляющих вектора 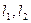ими однозначно порождается некоторый параллелограмм, а следовательно и плоскость. Одного направляющего вектора недостаточно, ведь тогда плоскость может вращаться вокруг него, то есть плоскость не будет однозначно фиксирована. Обозначим координаты направляющих, например, так: 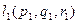и .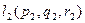

Первый способ. Можно найти нормаль к плоскости как векторное произведение 2 направляющих векторов 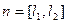и далее искать уравнение плоскости по точке и нормали, методом, рассмотренным в пункте 1. Но это будет решение в 2 шага.

Однако можно также получить уравнение плоскости сразу, без вычисления векторного произведения:

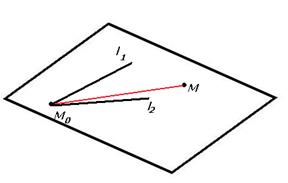
Второй способ. Возьмём произвольную точку . Если она принадлежит плоскости, то вектор (показан красным цветом) будет лежать в плоскости, то есть тройка векторов 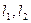, образует линейно-зависимую систему (ЛЗС), то есть эти векторы не образуют параллелепипед, а лежат в одной плоскости. Тогда смешанное произведение 0, то есть определитель, составленный из них, равен 0:

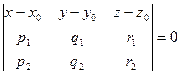
Вычисляя этот определитель, мы получим в качестве результата некоторое уравнение, содержащее x,y,z. А если начальная точка (0,0,0), то уравнение будет вычисляться с помощью такого определителя: .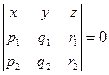

Пример. Построить уравнение плоскости, проходящей через начало координат, параллельно 2 направляющим (1,2,3) и (1,1,1).

Решение. 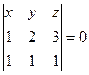. Можем разложить по первой строке: = .

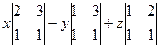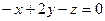Для удобства, чтобы 1-й коэффициент был положителен, можно домножить на 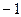. Ответ: .

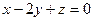Замечание. Векторы 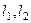можно поменять местами, и это не влияет на уравнение плоскости. Неважно, какой из них считается первым, а какой вторым. Если все миноры сменят знак, то из уравнения просто можно будет вынести коэффициент .

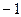Замечание. Построение уравнения плоскости по трём точкам. Если дано 3 точки, достаточно взять 2 направляющих 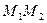и 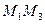(пусть это и будут те самые 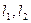) и затем действовать так, как сказано ранее.