2017-10-25
564
1. (Л1) Докажите лемму о том, что количество перестановок равно n!.
2. (Л2) Докажите свойство: Если все элементы какой-либо строки представлены в виде сумм двух элементов, то данный определитель равен сумме двух определителей:
= 
+ 
.
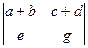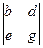3. (Л2) Докажите свойство: Если к любой строке прибавить другую строку, домноженную на число,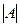 
не изменится.
4. (Л2) Докажите, что обратная матрица 
существует тогда и только тогда, когда А невырожденная.
5. (Л2) Докажите, что если матрица треугольная, то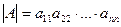 
.
6. (Л2) Докажите, что если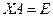 
и 
, то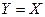 
.
Знать определения из лекции 3: что такое ранг матрицы; линейная комбинация; линейно-зависимая и линейно-независимая система векторов, базис и ранг системы векторов. Скалярное, векторное и смешанное произведение, метод вычисления векторного и смешанного произведений с помощью определителя. Основная и расширенная матрица системы линейных уравнений. Однородная и неоднородная системы, совместная и несовместная, определённая и неопределённая.
Формулировка теоремы Кронекера-Капелли (система совместна 
ранг основной матрицы равен рангу расширенной).
7. (Л3) Докажите теорему: Система линейно зависима хотя бы один из векторов этой системы является линейной комбинацией остальных.
8. (Л4) Доказательство формул Крамера.
9. (Л4) Доказательство теоремы о наложении решений.
10. (Л4) Доказать теорему: Линейная комбинация решений однородной системы тоже есть решение.
11. (Л4) Доказать теорему: Сумма решений неоднородной и соответствующей однородной системы есть решение неоднородной системы.
12. (Л5) Доказать теорему: Линейная комбинация собственных векторов, соответствующих одному и тому же числу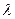 
, тоже является собственным вектором, соответствующим .
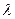13.(Л5) Доказать теорему: Любые два собственных вектора, соответствующих различным собственным числам, образуют ЛНС (линейно-независимую систему).
14.(Л5) Доказать теорему: Если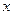 
является собственным вектором линейного оператора 
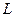, соответствующим 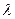, то он также является собственным и для обратного оператора 
, и соответствует числу 
.
15.(Л5) Доказать теорему: Число 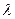является собственным для линейного оператора, заданного матрицей 
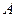, тогда и только тогда, когда 
.
16.(Л5) Доказать теорему: Если базис состоит из собственных векторов, то матрица оператора в этом базисе диагональна.
17.(Л5) Доказать теорему: Матрица А симметрична (то есть 
) выполняется свойство (Ax,y) = (x,Ay).
18. (Л5) Доказать теорему: Собственные векторы симметрического оператора, соответствующие разным 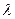, ортогональны.
Что такое билинейная форма, квадратичная форма, привести какой-либо пример квадратичной формы и её матрицы.
19. (Л6) Вывести уравнение прямой (либо уравнение плоскости - на ваш выбор) по точке и нормали. Доказать при этом, что координаты нормали будут коэффициентами в этом уравнении.
20. (Л6) Вывести уравнение прямой по точке и направляющему вектору (либо уравнение плоскости по точке и 2 направляющим).
21. (Л6) Вывести формулу проекции вектора на ось.
22. (Л6) Вывести формулу расстояния от точки до прямой в плоскости (либо от точки до плоскости в пространстве - на ваш выбор).
Литература.
1. Л.И.Магазинников, А.Л. Магазинникова.
Линейная алгебра. Аналитическая геометрия. Учебное пособие http://edu.tusur.ru/publications/2244
2. Л.И.Магазинников, А.Л.Магазинников.
Дифференциальное исчисление. Учебное пособие http://edu.tusur.ru/publications/2246
3. Магазинников Л.И. Высшая математика I. Практикум по линейной алгебре и аналитической геометрии: Учебное пособие Томск: ТУСУР, 2007. - 162 с.
Все учебные пособия кафедры математики можно найти на сайте кафедры по ссылке: http://math.tusur.ru/book.html
