1. Определение производной функции. Правила дифференцирования.
Упражнения:
Найти производные первого порядка данных функций: 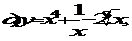
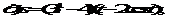
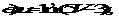
2.Решение задач на вычисление производной сложной функции.
Упражнения: 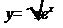 y = ln2 x2
y = ln2 x2
y = 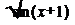 y = cos (e
y = cos (e 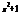 ) y = cos2 (ln3x) y = ln(sin6x) y = sin (x2-5x+1)
) y = cos2 (ln3x) y = ln(sin6x) y = sin (x2-5x+1)
3.Вычисление второй производной и производных высших порядков.
Упражнения:
1. Найти производные второго порядка данных функций: 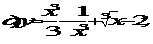
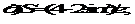
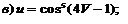
2. Найти производные второго и третьего порядка функции 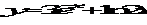 , у= sin 2x-cos 3x,
, у= sin 2x-cos 3x, 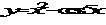 , у=3х4-5х3+12.
, у=3х4-5х3+12.
Тема 3. Интегральное исчисление.
1. Нахождение неопределенных интегралов методом непосредственного интегрирования.
Упражнения:
1. Вычислить интегралы:
1) 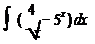 ; 2)
; 2) 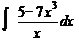 ;3)
;3) 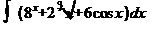 ; 4)
; 4) 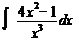 ;
;
2. Нахождение неопределенных интегралов методом введения вспомогательной переменной.
Упражнения:
1. Вычислить интегралы:
1) 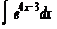 ; 2)
; 2) 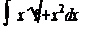 , 3)
, 3) 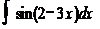 ; 4)
; 4) 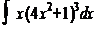 .
.
3. Нахождение неопределенных интегралов методом интегрирования по частям.
Упражнения:
1. Вычислить интегралы:
1)  ; 2)
; 2) 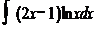 ; 3)
; 3) 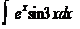 .
.
4 ) 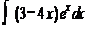 ; 5)
; 5) 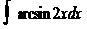 ; 6)
; 6) 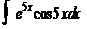 .
.
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ОБУЧАЮЩИХСЯ ПО ДИСЦИПЛИНЕ
Материалы представлены в Положении о самостоятельной работе обучающихся.
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ ОБУЧАЮЩИХСЯ ПО ДИСЦИПЛИНЕ
 2017-11-30
2017-11-30 414
414








