
 Теорема Ферма. Пусть f(x) задана на открытом промежутке и достигает в
Теорема Ферма. Пусть f(x) задана на открытом промежутке и достигает в  своего max(min), тогда если f(x) имеет f´(x), то она равна 0. Доказательство:
своего max(min), тогда если f(x) имеет f´(x), то она равна 0. Доказательство:
Допустим 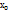 точка maх; f´(
точка maх; f´( )=
)=  ∆f=(f(
∆f=(f( +∆x)-f(
+∆x)-f( ))≤0 + ∆x
))≤0 + ∆x
 1)∆x
1)∆x  0 ∆f ˂0 следовательно
0 ∆f ˂0 следовательно  ˂ 0
˂ 0 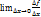 =f´(x) ≤ 0 2)∆x˂0 ∆f
=f´(x) ≤ 0 2)∆x˂0 ∆f  0 следовательно
0 следовательно 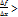 0
0 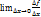 =f´(x)
=f´(x)  0
0
Из этих условий следует, что f´(x)=0
Теорема Ролля. Если функция f(x) непрерывна на отрезке  , дифференцируема во всех точках интервала (a;b) и на концах x=a и x=b принимает равные значения (f(a)=f(b)), то существует внутри интервала (a;b) по крайней мере одна точка x=c, a˂c˂b, в которой производная f´(х) обращается в ноль, т.е. f´(с)=0Доказательство:
, дифференцируема во всех точках интервала (a;b) и на концах x=a и x=b принимает равные значения (f(a)=f(b)), то существует внутри интервала (a;b) по крайней мере одна точка x=c, a˂c˂b, в которой производная f´(х) обращается в ноль, т.е. f´(с)=0Доказательство:
Рассмотрим два случая: 1 ) Если непрерывна на  , то по второй теореме Вейерштрасса. М-наиб. m-наим. M=m следовательно f(x)-const. F´(x)=0, x
, то по второй теореме Вейерштрасса. М-наиб. m-наим. M=m следовательно f(x)-const. F´(x)=0, x  (a;b) 2)Если m˂M то хотя бы одно из значений функции достигает внутри промежутка. Значит это локальный экстремум. Следовательно по теореме Ферма f´(c)=0Теорема Ролля имеет наглядный физический смысл. Предположим, что тело движется вдоль прямой и через некоторый промежуток времени возвращается в исходную точку. Тогда в данном промежутке времени существует момент, в котором мгновенная скорость тела была равна нулю.
(a;b) 2)Если m˂M то хотя бы одно из значений функции достигает внутри промежутка. Значит это локальный экстремум. Следовательно по теореме Ферма f´(c)=0Теорема Ролля имеет наглядный физический смысл. Предположим, что тело движется вдоль прямой и через некоторый промежуток времени возвращается в исходную точку. Тогда в данном промежутке времени существует момент, в котором мгновенная скорость тела была равна нулю.
Теоремы Ферма и Ролля
|
|

Сейчас читают про:
 2017-10-25
2017-10-25 998
998







