2017-10-25
2431
Теорема Лагранжа: Если функция f(x) удовлетворяет условиям:
1. Функция непрерывна на 
2. Функция дифференцируема на 
, то существует 
(a;b) такая что f(b)-f(a)=f´( 
)*(b-a) Доказательство:
Рассмотрим вспомогательную функцию 
Эта функция непрерывна и дифференцируема в промежутке [a;b], а на его концах принимает одинаковые значения: F(a)=F(b)=0
Тогда F(x) удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка (a;b), в которой производная функции F(x) равна нулю:
геометрический смысл: геометрический смысл теоремы Лагранжа таков: на графике функции f(x) найдется точка С(с, f(с)), в которой касательная к графику f(x) параллельна секущей АВ. Следствия:1. Если f'(х) = 0 на некотором промежутке (a, b), то функция f(x) постоянна на этом промежутке. 2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Теорема Коши: Если 1) f(x) и g(x) непрерывны на 2) f(x) и g(x) дифференцируемы на (a;b) 3) g´(x) 
0 на . то существует точка С 
такая что 
= 
. Следствие: теорема Лагранжа является частным случаем теоремы Коши при g(x)=x.
|
|
|
22. Теорема Лопиталя.
f(x), g(x) определены в некоторой окрестности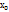 
за исключением может быть самой точки и удовлетворяет условиям 1) f(x) и g(x)- дифференцируемы
2) g´(x) 0, то существует формула 
и 
3) справедлива формула 
= 
= 
= 
; = = 
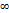Пример: 
= 
= 
= 
= 
; 
= 
= 
= 
...= 
=0 3) 
= 
= 
= 
= 
Теорема Тейлора.
Если f(x) имеет в некоторой окрестности точку 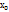, производную (n+1) порядка, существует 
окр. 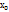, f(x)= 
+ 
(x), где (x)= 
* 
Пример: Найти формулу Тейлора для функции у= 
при 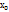=0. y´= 
; y´(0)=1; 
= ; y´(0)=1; 
= 
; 
; = 
+ 
; = 
+ 
; =1+ 
+ 
+ 
...+ 
+ 
(x).
