Если функция f(х) диф. на интервале (a;b) и f´(x)≥0 (f(x)≤0) для любых х  (a;b), то функция не убывает(не возрастает) на этом интервале. Доказательство: на интервале (a;b) выполнены все условия теоремы Лагранжа для любых
(a;b), то функция не убывает(не возрастает) на этом интервале. Доказательство: на интервале (a;b) выполнены все условия теоремы Лагранжа для любых 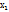 ,
, 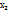 , f(a;b);
, f(a;b);  . f(
. f(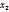 )-f(
)-f(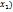 =f´(C)(
=f´(C)(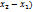 ;f´(C)≥0,(
;f´(C)≥0,( ;C
;C 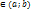 ; f(
; f(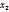 )-f(
)-f(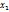 )≥0 следовательно f(
)≥0 следовательно f( ≥f(
≥f(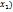 Функция не убывающая, ч.т.д. Т(
Функция не убывающая, ч.т.д. Т(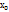 ,f(
,f(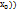 -называется точкой локального max(min), если существует ∆-окрестность в точки
-называется точкой локального max(min), если существует ∆-окрестность в точки 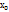 такая, что для любых х из этой окрестности выполняется неравенство f(
такая, что для любых х из этой окрестности выполняется неравенство f( )
)  Необходимое условие локального экстремума. Если f(x) имеет в точке
Необходимое условие локального экстремума. Если f(x) имеет в точке  локальный экстремум и диф. в этой точке, то f´(
локальный экстремум и диф. в этой точке, то f´( )=0. Доказательство данной теоремы основано на теореме Ферма. Пример:y=
)=0. Доказательство данной теоремы основано на теореме Ферма. Пример:y= 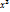 ;y´(x)=3
;y´(x)=3 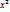 ; 3
; 3 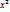 =0; x=0. Достаточное условие локального экстремума: Если f(x) диф. в некоторой окрестности точки
=0; x=0. Достаточное условие локального экстремума: Если f(x) диф. в некоторой окрестности точки 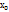 и опр. в ней, то
и опр. в ней, то
1) f´(x) 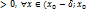 ) - Max
) - Max
f´(x) 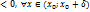
2) f´(x)  ) - Min
) - Min
f´(x) 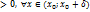
Доказательство основано на теореме Лагранжа.
y= 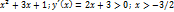
 2017-10-25
2017-10-25 436
436








