Направление выпуклости

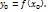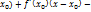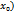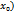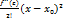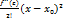Если функция f(x) имеет на (a;b) вторую производную и f´´(x) 0 (f´´(x) 0) , то график функции имеет выпуклость направленную вниз(вверх). Доказательство Запишем уравнение касательной R в точке ; y=f( уравнение касательной. Рассмотрим интервал (a;b) на нёразложим по формуле Тейлора y=f( + (x- + ; ; Y-y= ; y-Y ; y-Y , y 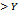Точки перегиба графика функции: () называется точкой перегиба графика функции y=f(x), если график имеет в этой точке касательную и разные напр. выпуклости слева и справа от этой точки.

Необходимые условия точки перегиба.

Если функция y=f(x) имеет в точке 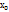перегиб и непрерывную производную в некоторой окрестности этой точки, то вторая производная в этой точке равна 0. Доказательство: производится от обратного предположения, что вторая производная не равна 0. По теореме о сохранение знака сущ. окрестность, в которой функция имеет тот же знак, что и в точке 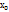, а это противоречит условию теоремы. Достаточное условие точки перегиба: для того чтобы имела в точке 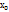перегиб, достаточно, чтобы она имела f´´ и разные направления выпуклости слева и справа от этой точки.