
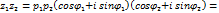
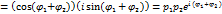
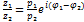
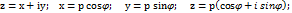
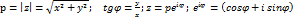
φ=Arg Z=2  0
0 
z=1, x=1; y=0; p= 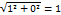
cos  =1; tg
=1; tg 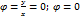
z=1(cos 0+ i sin 0)= cos 0+ i sin 0 = 1+i
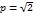 ; tg
; tg 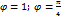
z=1+i=  )
)
Возведение комплексного числа в степень и извлечение корня.
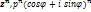

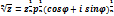
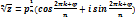
k=0,1,2,..,n-1
Формулы Эйлера:
Формула Эйлера утверждает, что для любого действительного и комплексного числа x выполнено следующее равенство: eix = cos x + sin x, где е — одна из важнейших математических констант, определяющаяся следующей формулой:  , i — мнимая единица.
, i — мнимая единица.
Доказательство формулы Эйлера можно провести с использованием рядов Тейлора. Разложим функцию eix в ряд Тейлора в окрестности точки a = 0 по степеням x. Получим:
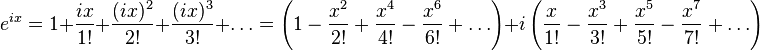
Но
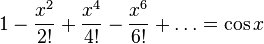

Поэтому eix = cos x + sin x ч. т. д.
Матрицы и действия над ними.
Определители второго и третьего порядков.
Миноры и алгебраические дополнения.
Обратная матрица
Решение систем линейных алгебр. уравнений. Теорема Крамера.
Линейная балансовая модель Леонтьева.
Метод Гаусса-Жордана.
Ранг матрицы. Теорема Кронекера-Капелли.
Прямоугольная система координат в пространстве. Понятие вектор. Проекция вектора на ось. Направляющие косинусы вектора.
Линейные операции над векторами. Теоремы о проекциях векторов. Линейная зависимость векторов.
Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
Векторное произведение. Выражение векторного произведения через координаты векторов.
 2017-10-25
2017-10-25 550
550








