Асимптоты- прямая, к которой график функции сколь угодно раз близко приближается при х 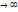 или в окрестности точек разрыва. Асимптоты бывают: вертикальными, горизонтальными, наклонными. Горизонтальная асимптота: прямая у=
или в окрестности точек разрыва. Асимптоты бывают: вертикальными, горизонтальными, наклонными. Горизонтальная асимптота: прямая у= 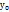 графика f(х) если
графика f(х) если 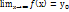 . Прямая х=
. Прямая х= 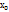 называется вертикальной асимптотой графика у=f(х), если хотя бы один из односторонних пределов
называется вертикальной асимптотой графика у=f(х), если хотя бы один из односторонних пределов 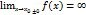 . у=
. у= 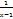 ;
; 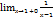 =+
=+ 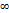 ;
; 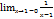 =-
=- 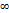 . у=
. у= 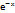 ;
; 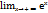 =
= 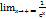 =0, у=0- горизонтальная асимптота.
=0, у=0- горизонтальная асимптота.
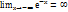 . Наклонная асимптота- это прямая у=kx+b график функции у=f(x) при f(x)=kx+b+
. Наклонная асимптота- это прямая у=kx+b график функции у=f(x) при f(x)=kx+b+  , x
, x 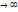 , где
, где 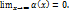 k=
k= 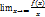 ; b=
; b= 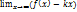 . Если хотя бы один из пределов не существует или бесконечен, то наклонной асимптоты нет. Пример: y=
. Если хотя бы один из пределов не существует или бесконечен, то наклонной асимптоты нет. Пример: y= 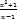 ; k=
; k= 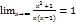 ; у=
; у= 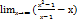 =
=  =
= 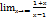 =1
=1
y=1*x+1=x+1 Cхема исследования графика функции. 1) Область определения, область значения, чётность, не чётность, периодичность. 2) Характерные точки графика функции(пересечение с осями)- х=0,у=0. 3) Точки возможного экстремума. f´(x)=0. Интервалы монотонности f´(x) 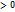 , f´(x)
, f´(x)  4) Точки перегиба:f´´(x)=.0 Направление выпуклости f´´(x)
4) Точки перегиба:f´´(x)=.0 Направление выпуклости f´´(x) 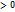 ; f´´(x)˂0. 5) Асимптоты графика функции 6) Построение графика на основании исследования.
; f´´(x)˂0. 5) Асимптоты графика функции 6) Построение графика на основании исследования.
28. Комплексные числа. 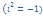
- это упорядоченная пара действительных чисел. 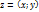 Комплексные числа- это расширенное понятие числа. z=(x;0)- действительное число, где х- действенная часть; у-мнимая часть. z=(0;у)- чисто мнимое число; z=(0;1)- мнимая единица-i;
Комплексные числа- это расширенное понятие числа. z=(x;0)- действительное число, где х- действенная часть; у-мнимая часть. z=(0;у)- чисто мнимое число; z=(0;1)- мнимая единица-i; 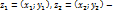 равные числа
равные числа 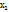 =
=  ;
;  Действие над комплексными числами Суммой(разностью) 2-х комплексных чисел называется число, определяемое следующим образом: z=
Действие над комплексными числами Суммой(разностью) 2-х комплексных чисел называется число, определяемое следующим образом: z=  Комплексное число может быть представлено в виде: z=x+iy(алгебраическая форма)=(
Комплексное число может быть представлено в виде: z=x+iy(алгебраическая форма)=( 
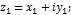

z= 
 +i
+i 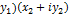 = (
= (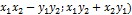
 )
)
 2017-10-25
2017-10-25 424
424








