sin2x+cos2x=1
tg2x+1= 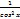 ctg2x+1=
ctg2x+1= 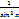 tgx=
tgx= 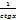 tgx*ctgx=1
tgx*ctgx=1
| tgx= 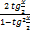 sinx=
sinx= 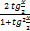 cosx=
cosx= 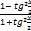
| 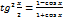
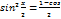
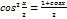
| cos(-α)=cos α
sin(-α)=-sin α
tg(-α)=-tg α
ctg(-α)=-ctg α
|
sin2x=2 sinx cosx
sin3x=2sinx-4sin3x
sin4x=2sin2x–cos2x
cos2x=cos2x-sin2x cos2x=2cos2x-1
cos2x=1-2sin2x
cos3x=4cos3x-3cosx
tg2x= 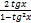 tg3x=
tg3x= 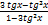
| cos(π/2-x)=sin x
cos(π±x)=-cos x
cos(π/2+x)=-sin x
cos(3π/2-x)=-sin x
cos(3π/2+x)=sin x
| sin(π/2±x)=cos x
sin(π-x)=sin x
sin(π+x)=-sin x
sin(3π/2±x)=-cos x
|
| tg(π/2+x)=-ctg x
tg(π/2-x)=ctg x
ctg(π/2+x)=-tg x
ctg(π/2-x)=tg x
| 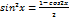 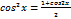
|
| )0)))
| sin(x+y)=sinx·cosy+cosx·siny
sin(x-y)=sinx·cosy-cosx·siny
cos(x+y)=cosx·cosy–sinx·siny
cos(x-y)=cosx·cosy+sinx·siny
tg(x+y)= 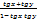 tg(x-y)= tg(x-y)= 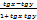
|
sinx+siny=2 sin(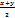 )·cos( )·cos(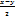 )
sinx-siny=2 sin( )
sinx-siny=2 sin(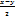 )·cos( )·cos(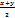 )
cosx+cosy=2 sin( )
cosx+cosy=2 sin(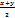 )·sin( )·sin(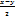 )
cosx+cosy=-2 sin( )
cosx+cosy=-2 sin(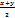 )·sin( )·sin(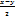 ) )
|
| | | | | | | | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| sin
|
| 
| 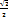
| 
|
| 
| 
| 
|
| 
| 
| 
| -1
| 
| 
| 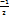
|
|
| cos
|
| 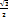
| 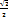
| 
|
| 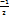
| 
| 
| -1
| 
| 
| 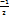
|
| 
| 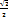
| 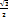
|
|
| tg
|
| 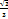
|
| 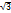
| -
| - 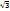
| -1
| 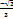
|
| 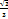
|
| 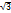
| -
| 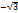
| -1
| 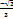
|
|
| ctg
| -
| 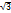
|
| 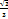
|
| 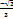
| -1
| - 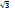
| -
| 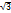
|
| 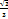
|
| 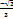
| -1
| 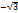
| -
|
| arc
|
| 
| 
| 
| 
| 
| 
| 
| π
| 
| 
| 
| 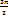
| 
| 
| 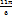
| 2π
|
| х2 - у2 = (х - у) (х+у)
(х + у)2 = х2 + 2ху + у2
(х - у)2 = х2 – 2ху + у2
(х + у)3 = х3 + 3х2у + 3ху2 + у3
(х - у)3 = х3 – 3х2у + 3ху2 - у3
х3 + у3 = (х + у) (х2 - ху + у2)
х3 - у3 = (х - у) (х2 + ху + у2)
| alogab = b
loga 1 = 0
loga a = 1
| logax= 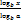 logax=
logax= 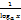
|
loga(x · y) = logax + logay
loga xy = logax - logay
loga xp = p logax
logak x =  loga x, при k ≠ 0 loga x, при k ≠ 0
|
(f(x)+g(x))’=f ’(x)+g’(x)
(k•(f(x))’ = k•f ’(x)
(f(x)•g(x))’=f ’(x)·g(x)+f(x)·g’(x)
(f(x)/g(x))’= 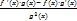 (f(g(x))’=f ‘(g(x))•g’(x)
lim f(x)g(x)=
(f(g(x))’=f ‘(g(x))•g’(x)
lim f(x)g(x)= 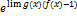 lim ex = ∞, x→+∞; 0, x→-∞
lim ex = ∞, x→+∞; 0, x→-∞
| при 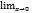 sin x ̴x
arccsin x ̴x
tg x ̴x
arctg x ̴x 1-cos x ̴ x2/2 sin x ̴x
arccsin x ̴x
tg x ̴x
arctg x ̴x 1-cos x ̴ x2/2
|
ax ̴1+x lna
ex-1 ̴x
ln (1+x) ̴x
loga(1+x) ̴x/lna
(1+x)m-1 ̴mx
|
| lim (1+x)1/x=e
|
| | | | | | | | | | | | | | | | | | | |
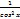 ctg2x+1=
ctg2x+1= 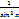 tgx=
tgx= 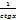 tgx*ctgx=1
tgx*ctgx=1
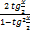 sinx=
sinx= 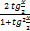 cosx=
cosx= 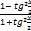
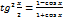
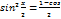
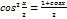
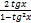 tg3x=
tg3x= 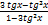
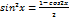
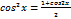
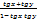 tg(x-y)=
tg(x-y)= 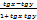
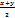 )·cos(
)·cos(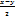 )
sinx-siny=2 sin(
)
sinx-siny=2 sin(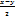 )·cos(
)·cos(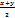 )
cosx+cosy=2 sin(
)
cosx+cosy=2 sin(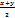 )·sin(
)·sin(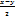 )
cosx+cosy=-2 sin(
)
cosx+cosy=-2 sin(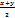 )·sin(
)·sin(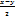 )
)

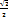
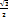
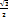
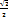

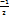
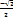
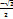
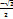
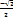
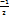
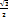
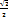

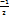
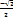
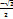
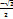
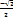
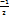

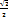
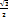
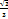
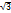
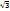
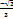
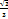
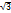
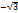
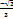
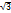
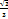
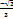
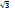
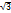
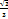
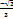
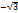










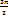


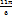
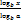 logax=
logax= 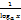
 loga x, при k ≠ 0
loga x, при k ≠ 0
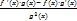 (f(g(x))’=f ‘(g(x))•g’(x)
lim f(x)g(x)=
(f(g(x))’=f ‘(g(x))•g’(x)
lim f(x)g(x)= 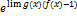 lim ex = ∞, x→+∞; 0, x→-∞
lim ex = ∞, x→+∞; 0, x→-∞
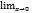 sin x ̴x
arccsin x ̴x
tg x ̴x
arctg x ̴x 1-cos x ̴ x2/2
sin x ̴x
arccsin x ̴x
tg x ̴x
arctg x ̴x 1-cos x ̴ x2/2
 2017-10-25
2017-10-25 379
379







