Два центробежных насоса подобны, если их сходственные параметры пропорциональны и равны критерии подобия.
Представим перечнь параметров, характеризующих динамические насосы:
 - диаметр (или другой характерный размер насоса),
- диаметр (или другой характерный размер насоса), 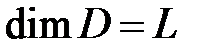 ;
;
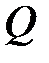 - объемный расход (подача) насоса,
- объемный расход (подача) насоса,  ;
;
 - частота вращения рабочего колеса,
- частота вращения рабочего колеса,  ;
;
 - напор, создаваемый насосом,
- напор, создаваемый насосом, 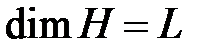 ;
;
 - плотность жидкости,
- плотность жидкости,  ;
;
 - кинематическая вязкость жидкости,
- кинематическая вязкость жидкости,  ;
;
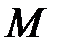 - момент на валу насоса,
- момент на валу насоса, 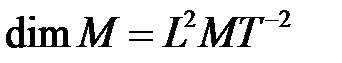 ;
;
 - гидравлическая мощность насоса,
- гидравлическая мощность насоса,  .
.
В качестве основных величин выберем плотность жидкости  , диаметр
, диаметр  и частоту вращения
и частоту вращения  . Проверим независимость их размерностей относительно размерностей основных величин системы
. Проверим независимость их размерностей относительно размерностей основных величин системы 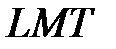 :
:

Определитель, составленный из показателей степеней,
 .
.
Поэтому размерности величин  являются независимыми.
являются независимыми.
Список параметров насоса представим следующим образом:
 .
.
В первой круглой скобке – основные величины, во второй – производные.Найдем критерии подобия. Количество критериев подобия: 8-3=5.
Критерий  будем искать в виде:
будем искать в виде:
 . (3.1)
. (3.1)
Уравнение размерностей
 .
.
Система уравнений для определения показателей степеней
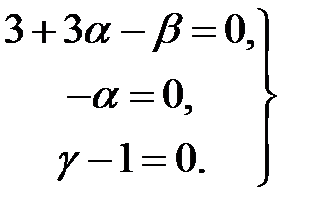
Отсюда  . Подставляя эти значения в выражение (3.1), получаем:
. Подставляя эти значения в выражение (3.1), получаем:
 . (3.2)
. (3.2)
Критерий подобия 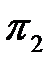 :
:
 . (3.3)
. (3.3)
Уравнение размерностей
 .
.
Уравнения для определения показателей степеней

дают следующие решения:  . Подставляя эти значения в (3.3), находим:
. Подставляя эти значения в (3.3), находим:
 . (3.4)
. (3.4)
Критерий подобия  :
:
 .
.
Уравнение размерностей
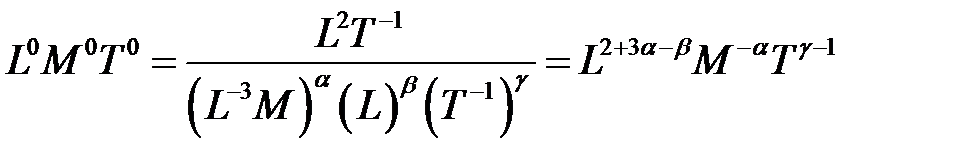 .
.
Система уравнений для показателей степени
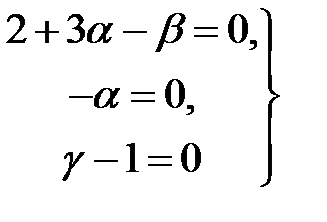
имеет следующее решение:  . Тогда для критерия подобия находим:
. Тогда для критерия подобия находим:
 . (3.5)
. (3.5)
Критерий подобия  :
:
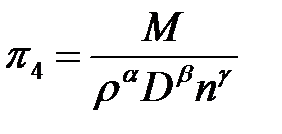 . (3.6)
. (3.6)
Уравнение размерностей
 .
.
Система уравнений для показателей

Её решение:  . С учетом этих значений критерий подобия (3.6) принимает вид:
. С учетом этих значений критерий подобия (3.6) принимает вид:
 . (3.7)
. (3.7)
Критерий подобия  :
:
 . (3.8)
. (3.8)
Уравнение размерностей
 .
.
Система уравнений для определения показателей степеней

Отсюда:  . Критерий подобия (3.8) окончательно принимает вид:
. Критерий подобия (3.8) окончательно принимает вид:
 . (3.9)
. (3.9)
Из полученных критериев подобия для двух подобных насосов следуют важные соотношения, используемые при расчетах центробежных насосов.
1. Из формулы (3.2) очевидно, что

или
 .
.
Отсюда
 . (3.10)
. (3.10)
2. Из выражения (3.7) получаем:
 ,
,
или
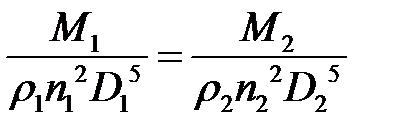 .
.
Отсюда
 . (3.11)
. (3.11)
3. Из формулы (3.9) находим:

или
 . (3.12)
. (3.12)
4. Из формул (3.10) и (3.12) получаем:
 , (3.13)
, (3.13)
 . (3.14)
. (3.14)
Так как  , то разделив выражение (3.14) на (3.13), находим формулу, связывающую напоры подобных насосов:
, то разделив выражение (3.14) на (3.13), находим формулу, связывающую напоры подобных насосов:
 .
.
Отсюда
 . (3.15)
. (3.15)
Выпишем формулы (3.10), (3.12) и (3.15), приняв в них  (жидкость, перекачиваемая подобными насосами одна и та же):
(жидкость, перекачиваемая подобными насосами одна и та же):
 ;
;  ;
;  . (3.16)
. (3.16)
Эти формулы позволяют производить пересчет параметров центробежных насосов с одной частоты вращения  и диаметра рабочего колеса
и диаметра рабочего колеса  на другую частоту
на другую частоту  и другой диаметр
и другой диаметр  .
.
Для одного и того же насоса  и формулы (3.16) принимают более простой вид:
и формулы (3.16) принимают более простой вид:
 ;
;  ;
;  . (3.17)
. (3.17)
Пример 1. Частота вращения центробежного насоса изменилась с  об/мин до
об/мин до  об/мин. Во сколько раз увеличится подача, напор и мощность насоса. Рассматриваются подобные режимы насоса.При этом
об/мин. Во сколько раз увеличится подача, напор и мощность насоса. Рассматриваются подобные режимы насоса.При этом  .
.
Формулы (3.17) приведем к виду:
 .
.
Вычислим отношение  .
.
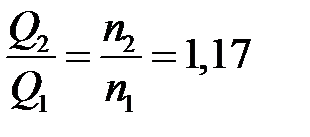 . Подача увеличится в 1,17 раза.
. Подача увеличится в 1,17 раза.
 . Напор увеличится в 1,36 раза.
. Напор увеличится в 1,36 раза.
 . Мощность увеличится в 1,6 раза.
. Мощность увеличится в 1,6 раза.
Пример 2. Центробежный насос с рабочим колесом, диаметр которого  мм, при частоте вращения
мм, при частоте вращения  об/мин создает напор
об/мин создает напор  м и подает жидкость с расходом
м и подает жидкость с расходом  л/с. Требуется определить частоту вращения
л/с. Требуется определить частоту вращения 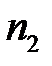 и диаметр
и диаметр  колеса насоса, который при подобном режиме работы создает напор
колеса насоса, который при подобном режиме работы создает напор 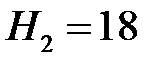 м и обеспечивает подачу
м и обеспечивает подачу  л/с.
л/с.
Для решения задачи будем использовать соотношения:
 ; (3.18)
; (3.18)
 . (3.19)
. (3.19)
Из формулы (3.18) найдем

и подставим в выражение (3.19):
 .
.
Отсюда

или
 мм.
мм.
Частоту вращения 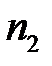 определим из формулы (3.18):
определим из формулы (3.18):
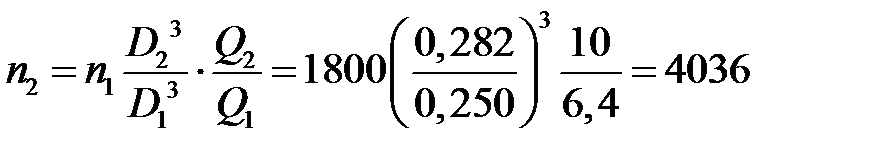 об/мин.
об/мин.
 2017-12-14
2017-12-14 1408
1408








