Рассмотрим основные этапы разработки физической модели потока жидкости. Схема моделируемого потока представлена на рис.3а.

Рис.3
Физическая модель потока изображена на рис.3б.
1. Схематизация потока жидкости. Она заключается в выборе тех физических величин, которые необходимы для полного (в рамках решаемой задачи) описания
потока. Пусть определяемыми величинами являются перепад давления на трубе  и скорость
и скорость 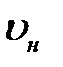 в заданной точке. Совокупность определяющих величин:
в заданной точке. Совокупность определяющих величин: 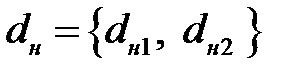 - диаметры трубы,
- диаметры трубы, 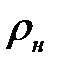 - плотность жидкости,
- плотность жидкости,  - осевые геометрические размеры,
- осевые геометрические размеры, 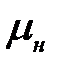 - динамическая вязкость жидкости.
- динамическая вязкость жидкости.
2. Величины, характеризующие процесс. Представим эти величины в виде списка, предварительно выбрав в качестве основных величин 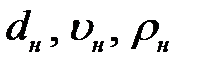 .Они имеют независимые размерности. Проверим независимость размерностей величин
.Они имеют независимые размерности. Проверим независимость размерностей величин  по отношению к основным единицам системы
по отношению к основным единицам системы 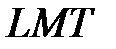 :
:
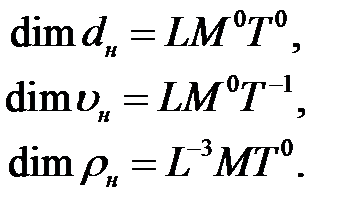
Действительно, определитель
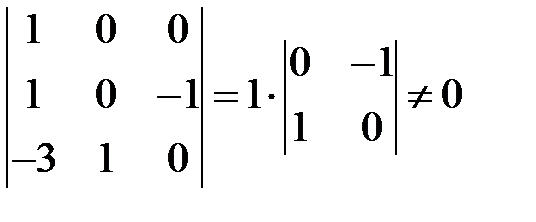 ,
,
а величины 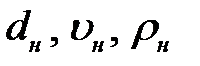 имеют независимые размерности.
имеют независимые размерности.
Список величин, характеризующих поток:
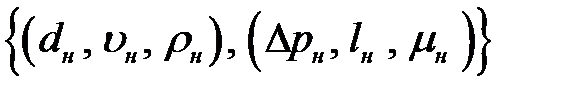 . (2.2)
. (2.2)
В первой круглой скобке – основные величины, во второй – производные.
3. Подобие рассматриваемых потоков будем устанавливать в духе третьей теоремы подобия. Для этого необходимо потребовать равенство критериев подобия и пропорциональность сходственных параметровобъекта и модели.
Сходственные параметры – это одноимённые параметры, принадлежащие моделируемому объекту (имеют нижний индекс «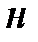 ») и модели (нижний индекс «
») и модели (нижний индекс «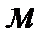 »).
»).
Воспользовавшись списком параметров (2.2), найдем критерии подобия. Согласно второй теореме подобия количество критериев равно трем. Для простоты нижние индексы при рассматриваемых величинах опустим.
1. Критерий 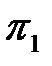 :
:
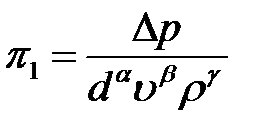 . (2.4)
. (2.4)
Уравнение размерностей
 .
.
Уравнения для определения показателей степени
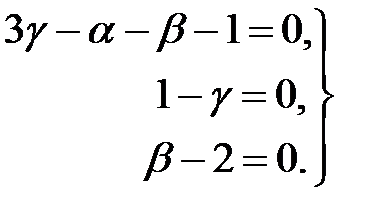
Отсюда: 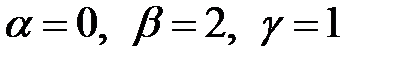 . Подставляя эти значения в (2.4), получаем:
. Подставляя эти значения в (2.4), получаем:
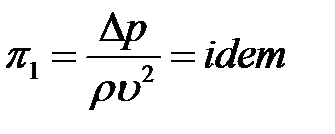 .
.
2. Критерий 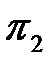 :
:
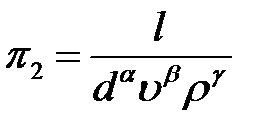 . (2.5)
. (2.5)
Уравнение размерностей
 .
.
Уравнения для определения показателей степени
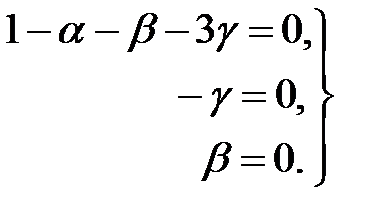
Отсюда: 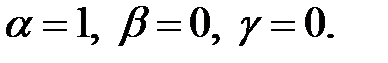 Подставляя эти значения в (2.5), находим:
Подставляя эти значения в (2.5), находим:
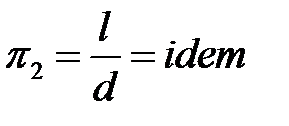 .
.
3. Критерий 
 . (2.6)
. (2.6)
Уравнение размерностей
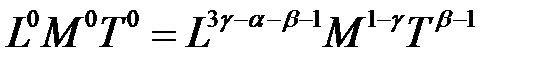 .
.
Уравнения для показателей степени
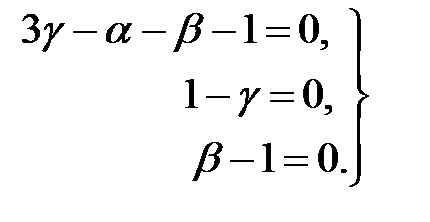
Отсюда следует: 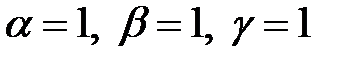 . Подставляя найденные значения показателей степеней в формулу (2.6), получаем:
. Подставляя найденные значения показателей степеней в формулу (2.6), получаем:
 .
.
Введем масштабные коэффициенты, устанавливающие пропорциональность сходственных параметров:
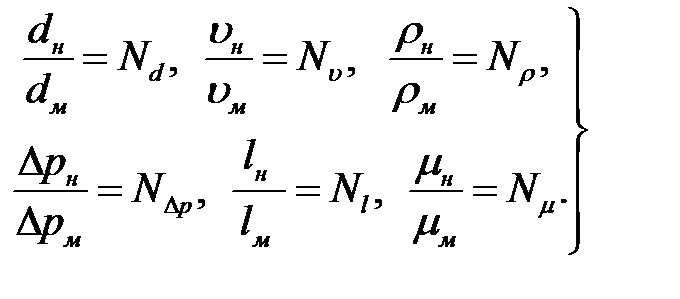 (2.3)
(2.3)
Выразим параметры моделируемого потока через параметры модели и масштабные коэффициенты (2.3):
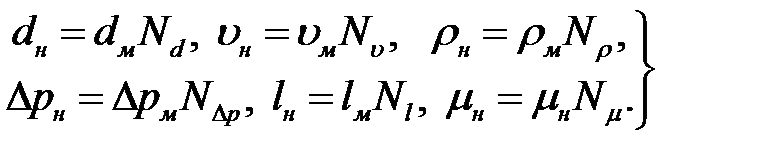 (2.7)
(2.7)
Критерии подобия 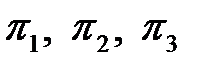 представим в виде:
представим в виде:
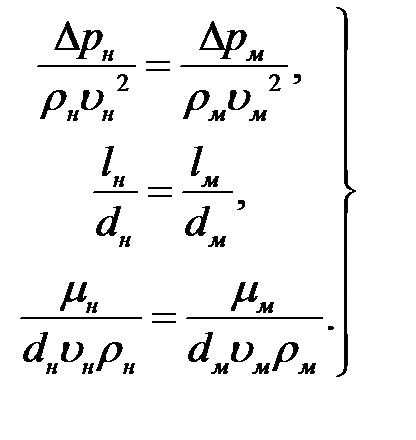 (2.8)
(2.8)
Подставим соотношения (2.7) в (2.8). В результате получаем:
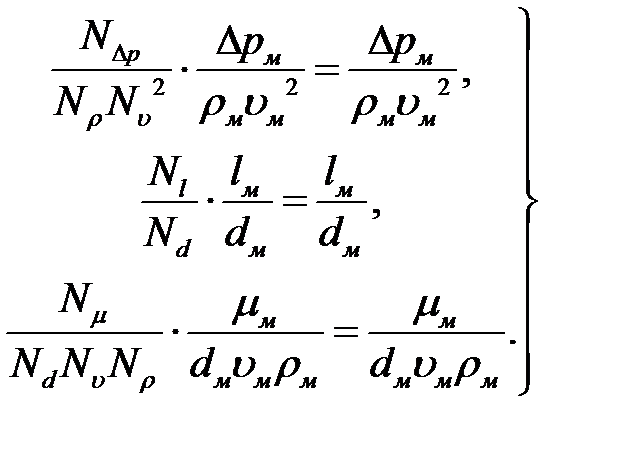 (2.9)
(2.9)
Для выполнения равенств (2.9) необходимо, чтобы комплексы из масштабных коэффициентов были равны единице:
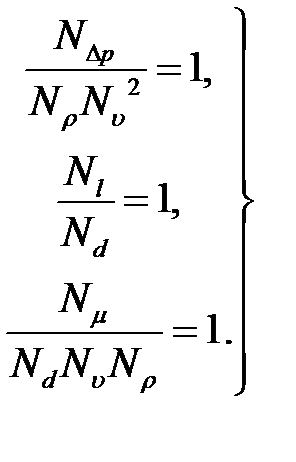 (2.10)
(2.10)
Соотношения (2.10) называются индикаторами подобия. На шесть масштабных коэффициентов (2.3) наложено три условия (2.10). Это означает, что три масштабных коэффициента могут быть заданы произвольно, исходя из параметров моделируемого потока и физической реализуемости модели, а остальные три должны быть определены из индикаторов подобия (2.10).
Пусть масштабные коэффициенты 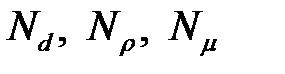 заданы. Остальные масштабные коэффициенты могут быть найдены из индикаторов подобия по формулам:
заданы. Остальные масштабные коэффициенты могут быть найдены из индикаторов подобия по формулам:
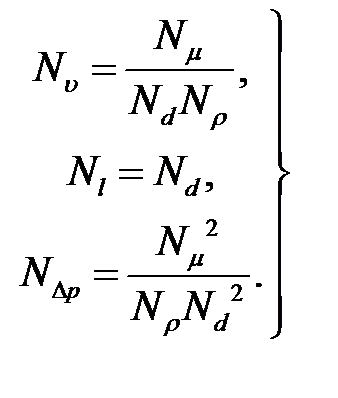 (2.11)
(2.11)
Соотношения (2.11) позволяют определить недостающие параметры модели и масштабные коэффициенты для перехода от измеренных в модели величин к сходственным величинам в моделируемом потоке.
По измеренным в модели параметрам 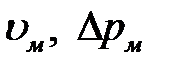 можно определить сходственные параметры в моделируемом потоке:
можно определить сходственные параметры в моделируемом потоке:
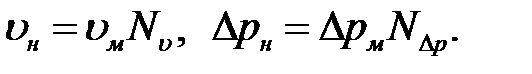
 2017-12-14
2017-12-14 1447
1447
