Для нахождения критериев подобия могут быть использованы следующие способы.
Первый способ заключается в анализе уравнений, описывающих подобные объекты. Вводятся коэффициенты пропорциональности сходственных физических величин – масштабные коэффициенты. Используя масштабные коэффициенты, параметры модели выражают через параметры объекта – оригинала. Затем подставляют их в уравнение, описывающее модель. Требуют тождественности полученного уравнения и уравнения оригинала. Отсюда получают индикаторы подобия, а затем критерии подобия.
Второй способ основан на анализе размерностей физических величин, характеризующих подобные объекты и не требует уравнений, описывающих модель и оригинал.
Подробно рассмотрим второй способ.
Необходимо найти критерии подобия двух потоков жидкости. Каждый из них описывается следующими параметрами:
 - линейные размеры,
- линейные размеры, 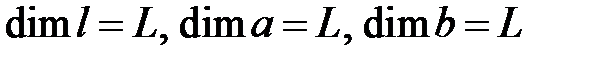 ;
;
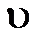 - характерная скорость,
- характерная скорость, 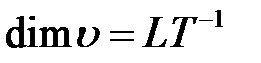 ;
;
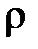 - плотность жидкости,
- плотность жидкости, 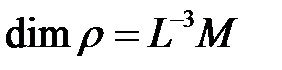 ;
;
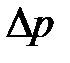 - перепад давления,
- перепад давления,  ;
;
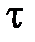 - касательное напряжение,
- касательное напряжение, 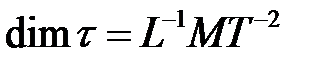 ;
;
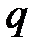 - ускорение свободного падения;
- ускорение свободного падения; 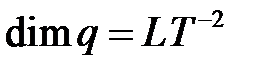 ;
;
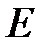 - модуль упругости жидкости,
- модуль упругости жидкости, 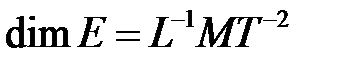 .
.
Список параметров позволяет установить, что всего физических величин 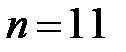 ; независимые размерности имеют три величины
; независимые размерности имеют три величины 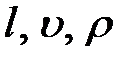 . Действительно, размерности величин
. Действительно, размерности величин
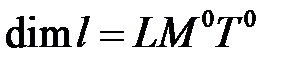 ,
,
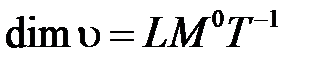 ,
,

являются независимыми относительно основных величин системы  , поскольку определитель, составленный из показателей степеней,
, поскольку определитель, составленный из показателей степеней,
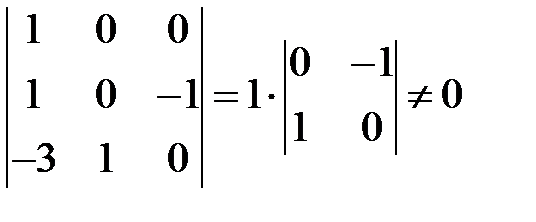 .
.
Так как 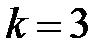 , то в соответствии со второй теоремой подобия количество критериев подобия будет равно
, то в соответствии со второй теоремой подобия количество критериев подобия будет равно 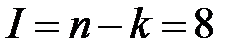 .
.
Как известно, критерий подобия – это безразмерный комплекс. Первый критерий подобия будем искать в виде:
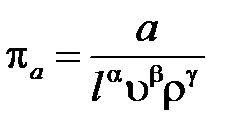 , (2.1)
, (2.1)
где 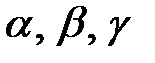 - показатели степеней, подлежащие определению.
- показатели степеней, подлежащие определению.
Очевидно, что

или
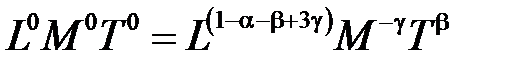 .
.
Приравнивая показатели степеней при одинаковых величинах в левой и правой частях последнего соотношения, находим систему уравнений для определения искомых показателей:
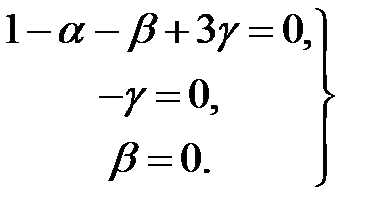
Отсюда следует: 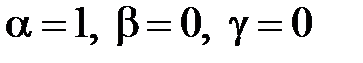 . Подставляя найденные показатели степеней в выражение (2.1), получаем:
. Подставляя найденные показатели степеней в выражение (2.1), получаем:
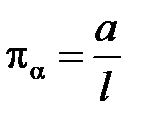 .
.
Аналогичным способом может быть найден второй критерий подобия:
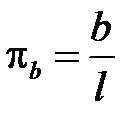 .
.
Следующий критерий подобия будем искать в виде
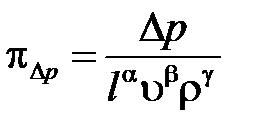 .
.
Для этого соотношения запишем уравнение размерностей
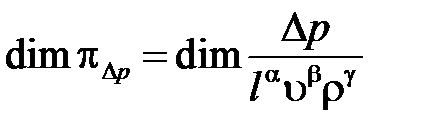
или
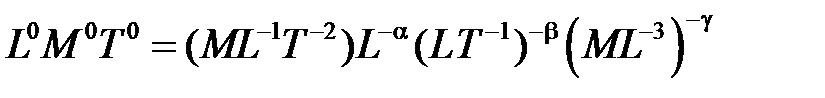 .
.
Приравнивая показатели степеней при одинаковых величинах в левой и правой частях, находим:
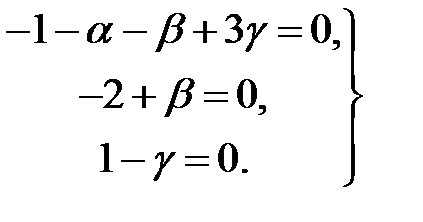
Решая эту систему, получаем: 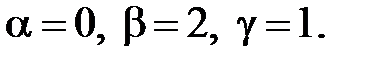 Следовательно
Следовательно
 .
.
Аналогичным образом находятся остальные критерии подобия:
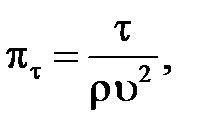
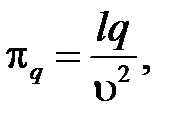
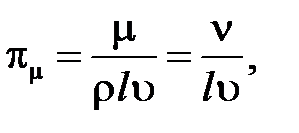
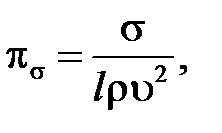
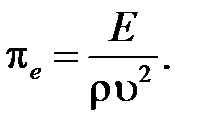
В соответствии с первой теоремой подобия у подобных потоков критерии подобия должны быть численно одинаковы:
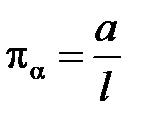
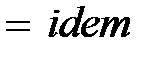 ,
,
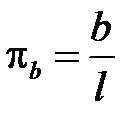
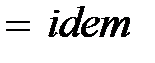 ,
,

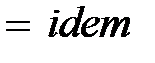 ,
,
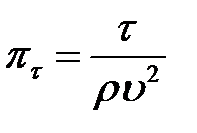
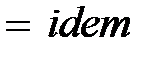 ,
,
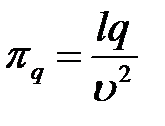
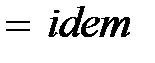 ,
,
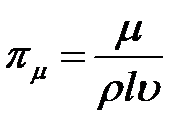
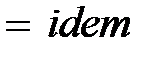 ,
,
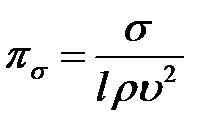
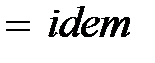 ,
,
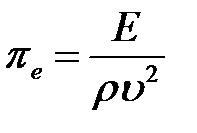
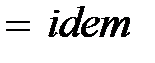 .
.
 2017-12-14
2017-12-14 1786
1786

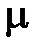 -
- 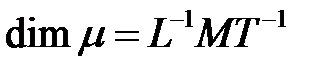 ;
; -
- 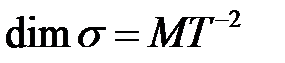 ;
;