2017-12-14
1651
Колебательных систем
В основе электрического моделирования колебаний механических систем лежит аналогия между различными по своей физической природе явлениями – механическими колебаниями и колебательными процессами в электрических цепях, состоящих и индуктивностей, трансформаторов, сопротивлений, конденсаторов, генераторов тока и напряжения[15]. При этом непосредственное исследование колебаний сложной механической системы, материальная реализация которой связана с определенными технико-экономическими трудностями, может быть заменено изучением колебательного процесса в электрической цепи, изготовление которой не требует особых затрат труда и средств. Приведем по этому поводу высказывание Н.Е. Жуковского: «…если одно из двух математически аналогичных явлений сложно и трудно наблюдается, а другое может быть осуществлено на простом приборе, то опытное изучение второго явления может расширить наше знакомство с первым, несмотря на то, что оба явления могут представлять неразрешимую математическую задачу».
|
|
|
Идею метода электромеханических аналогий рассмотрим на примере простых систем с одной степенью свободы. На рис.8 схематично изображена механическая колебательная система с одной степенью свободы.
Рис.8
Уравнение вынужденных колебаний системы имеет вид:
, (3.32)
где 
- масса объекта, кг;
- коэффициент сопротивления демпфера, 
;
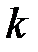- жесткость упругого элемента, 
;
- перемещение объекта относительно положения статического равновесия, м;
- внешняя вынуждающая сила,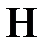 
;
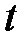- время, с.
Механической системе можно поставить в соответствие две дуальные (двойственные) электрические цепи: последовательный контур (рис. 9) и параллельный контур (рис. 10).
Рис.9
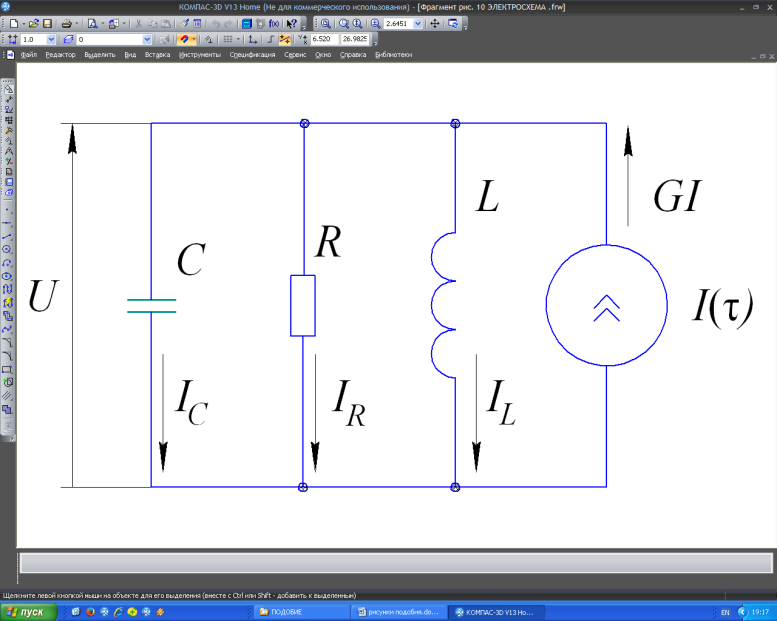
Рис.10
Используя законы Кирхгофа, можно получить уравнения, описывающие колебательные процессы в этих контурах.
