1739
При изучении двумерных случайных величин рассматриваются числовые характеристики составляющих:
, 
, 
, 
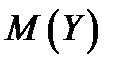, где
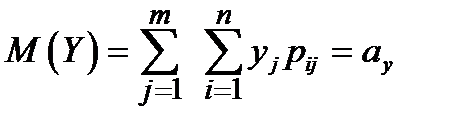
(6.2.1)
для дискретных составляющих X и Y и
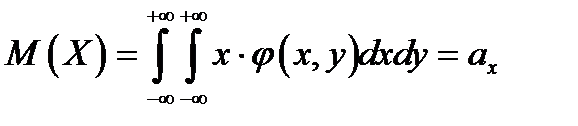
(6.2.2)
в случае непрерывных составляющих.
Упорядоченную пару чисел 
называют математическим ожиданием двумерной случайной величины, а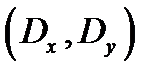 
- ее дисперсия.
Отмеченные выше числовые характеристики не определяют степень зависимости составляющих X и Y. Эту роль выполняют корреляционный момент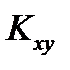 
(иначе: ковариация 
), который определяется следующим образом:
. (6.2.3)
Для дискретных случайных величин
(6.2.4)
Для непрерывных случайных величин
(6.2.5)
Корреляционный момент можно вычислить по формуле (6.2.6)
. (6.2.6)
Если Х и Y независимы, то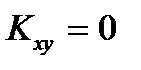 
. Если 
, то Х и Y зависимые случайные величины.
В случае 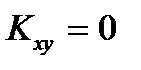случайные величины X и Y называют некоррелированными, при этом она могут быть как зависимыми, так и независимыми.
Ковариация X и Y характеризует не только степень зависимости случайных величин, но и их рассеяние вокруг точки . Кроме того, 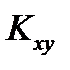- размерная величина, что затрудняет ее использование для оценки степени зависимости для различных случайных величин.
Для оценки зависимости вводится коэффициент корреляции
, (6.2.7) где 
и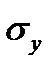 
- среднеквадратические отклонения X и Y.
Коэффициент корреляции 
- безразмерная величина, обладающая следующими свойствами:
1. - ограниченная величина, а именно 
.
2. Если X и Y – независимые случайные величины, то 
.
3. Если X и Y связаны линейной функциональной зависимостью 
, то 
и наоборот.
Из последнего свойства можно сделать вывод: коэффициент корреляции характеризует степень линейной зависимости случайных величин X и Y.
Пример 6.2.1.В урне содержится 4 белых и 2 черных шара. Из нее извлекают 2 шара без возвращения. Пусть X – число извлеченных белых шаров, Y – число извлеченных черных шаров. Составить закон совместного распределения двумерной случайной величины 
и найти коэффициент корреляции .
Решение. Как Х, так и Y могут принимать значения 0; 1; 2. Вычислим соответствующие вероятности.
, 
, 
.
| X Y | |||
| 0,4 | |||
| |||
|
Очевидно, что 
, 
, 
, 
, 
.
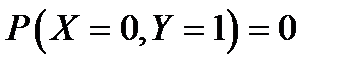
Составим распределения X и Y.
| X | |||
| pi |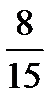 
| 
| 0,4 |
| Y | |||
| pj | 0,4 | 
| 
|
Найдем 
, 
.
Вычислим 
.
Вычислим 
и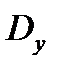 
.
.
Вычислим 
.
Следовательно, Х и Y связаны линейной зависимостью.
Пример 6.2.2. Плотность совместного распределения случайных величин Х и Y задана формулой
.
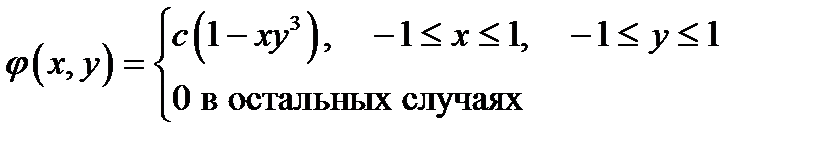Найти: 1) коэффициент с; 2) безусловные и условные плотности распределения Х и Y; 3) , 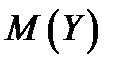; 4) ковариацию Х и Y.
Решение. Так как 
, то вычислив 
= 
, получим 
и 
.
Найдем 
и
.
Условный закон распределения Х
.
Аналогично,
.
Вычислим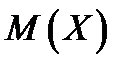 
и 
.
.
Аналогично 
.
Вычислим 
.
