Глава 6. Двумерные случайные величины.
Зачастую результат опыта описывается несколькими случайными величинами:  . Например, погоду в данном месте в определенное время суток можно охарактеризовать следующими случайными величинами: Х 1 – температура, Х 2 – давление, Х 3 – влажность воздуха, Х 4 – скорость ветра.
. Например, погоду в данном месте в определенное время суток можно охарактеризовать следующими случайными величинами: Х 1 – температура, Х 2 – давление, Х 3 – влажность воздуха, Х 4 – скорость ветра.
В этом случае говорят о многомерной случайной величине  или о системе случайных величин
или о системе случайных величин  .
.
Рассмотрим двумерную случайную величину  , возможные значения которой есть пары чисел
, возможные значения которой есть пары чисел  . Геометрически двумерную случайную величину можно истолковать как случайную точку на плоскости
. Геометрически двумерную случайную величину можно истолковать как случайную точку на плоскости 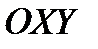 .
.
Если составляющие Х и Y – дискретные случайные величины, то  - дискретная двумерная случайная величина, а если Х и Y – непрерывные, то
- дискретная двумерная случайная величина, а если Х и Y – непрерывные, то  - непрерывная двумерная случайная величина.
- непрерывная двумерная случайная величина.
Законом распределения вероятностей двумерной случайной величины называют соответствие между возможными значениями и их вероятностями.
Закон распределения двумерной дискретной случайной величины может быть задан в виде таблицы с двойным входом (см. таблица 6.1), где  - вероятность того, что составляющая Х приняла значение xi, а составляющая Y – значение yj.
- вероятность того, что составляющая Х приняла значение xi, а составляющая Y – значение yj.
|
|
|
Таблица 6.1.1.
| Y X | y1 | y2 | … | yj | … | ym |
| x1 | p11 | p12 | … | p1j | … | p1m |
| x2 | p21 | p22 | … | p2j | … | p2m |
| … | … | … | … | … | … | … |
| xi | pi1 | pi2 | … | pij | … | pim |
| … | … | … | … | … | … | … |
| xn | pn1 | pn2 | … | pnj | … | pnm |
Так как события  , составляют полную группу попарно несовместных событий, то сумма вероятностей равна 1, т.е.
, составляют полную группу попарно несовместных событий, то сумма вероятностей равна 1, т.е.
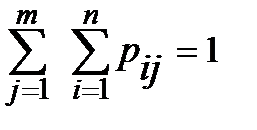 . (6.1.1)
. (6.1.1)
Из таблицы 6.1 можно найти законы распределения одномерных составляющих Х и Y.
Пример 6.1.1. Найти законы распределения составляющих Х и Y, если задано распределение двумерной случайной величины в виде таблицы 6.1.2.
Таблица 6.1.2.
| Y X | |||
| -1 | 0,11 | 0,13 | 0,23 |
| 0,1 | 0,12 | 0,09 | |
| 0,11 | 0,08 | 0,03 |
Решение. Так как
| -1 | ||
| 0,47 | 0,31 | 0,22 |

 , то проводя суммирование по строкам таблицы 6.1.2 получим распределение Х:
, то проводя суммирование по строкам таблицы 6.1.2 получим распределение Х:
Аналогично суммируя по столбцам, получим распределение Y:
| 0,32 | 0,33 | 0,35 |
Если зафиксировать значение одного из аргументов, например  , то полученное распределение величины Х называется условным распределением. Аналогично определяется условное распределение Y.
, то полученное распределение величины Х называется условным распределением. Аналогично определяется условное распределение Y.
Пример 6.1.2. По распределению двумерной случайной величины, заданной табл. 6.1.2, найти: а) условный закон распределения составляющей Х при условии  ; б) условный закон распределения Y при условии, что
; б) условный закон распределения Y при условии, что 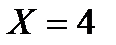 .
.
Решение. Условные вероятности составляющих Х и Y вычисляются по формулам
 ,
,  . (6.1.2)
. (6.1.2)
Тогда
а)  ,
, 
 ,
,
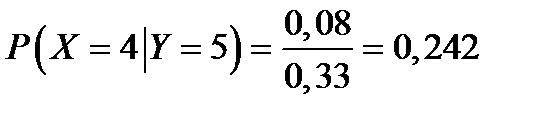 .
.
Условный закон распределения Х при условии  имеет вид
имеет вид
| -1 | ||
| 0,394 | 0,364 | 0,242 |
Контроль:  .
.
б) Аналогично находим условный закон Y при условии 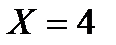 .
.
| 0,5 | 0,364 | 0,136 |
Контроль:  .
.
|
|
|
Закон распределения двумерной случайной величины  можно задать в виде функции распределения
можно задать в виде функции распределения  , определяющей для каждой пары чисел
, определяющей для каждой пары чисел 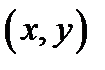 вероятность того, что Х примет значение, меньшее х, и при этом Y примет значение, меньшее y:
вероятность того, что Х примет значение, меньшее х, и при этом Y примет значение, меньшее y:
 . (6.1.3)
. (6.1.3)
Геометрически функция  означает вероятность попадания случайной точки
означает вероятность попадания случайной точки  в бесконечный квадрат с вершиной в точке
в бесконечный квадрат с вершиной в точке  (рис. 6.1.1).
(рис. 6.1.1).
y

x
-
Рис. 6.1.1.
Отметим свойства  .
.
1. Область значений функции  -
- 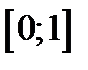 , т.е.
, т.е. 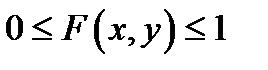 .
.
2. Функция  - неубывающая функция по каждому аргументу.
- неубывающая функция по каждому аргументу.
3. Имеют место предельные соотношения:
 ;
;  ;
; 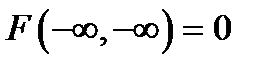 ;
;  .
.
При  функция распределения системы становится равной функции распределения составляющей Х, т.е.
функция распределения системы становится равной функции распределения составляющей Х, т.е.
 .
.
Аналогично,  .
.
Зная  , можно найти вероятность попадания случайной точки
, можно найти вероятность попадания случайной точки  в пределы прямоугольника ABCD (рис. 6.1.2).
в пределы прямоугольника ABCD (рис. 6.1.2).
y
B(x1,y2) C(x2,y2)
A(x1,y1) D(x2,y1)
x
Рис. 6.1.2.
А именно,
 =
= 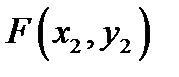


 . (6.1.3)
. (6.1.3)
Пример 6.1.3. Двумерная дискретная случайная величина задана таблицей распределения
| Y X | |||
| -1 | 0,17 | 0,11 | 0,09 |
| 0,27 | 0,10 | 0,26 |
Найти функцию распределения  .
.
Решение. Значение  в случае дискретных составляющих Х и Y находится суммированием всех вероятностей
в случае дискретных составляющих Х и Y находится суммированием всех вероятностей 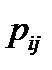 с индексами i и j, для которых
с индексами i и j, для которых  ,
, 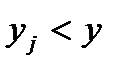 . Тогда, если
. Тогда, если  и
и  , то
, то 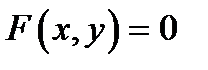 (события
(события 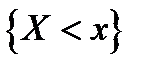 и
и 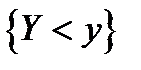 - невозможны). Аналогично получаем:
- невозможны). Аналогично получаем:
если  и
и  , то
, то 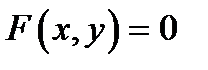 ;
;
если  и
и  , то
, то 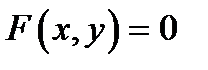 ;
;
если  и
и  , то
, то  ;
;
если  и
и 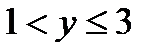 , то
, то 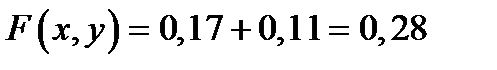 ;
;
если  и
и  , то
, то  ;
;
если 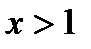 и
и  , то
, то 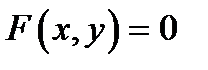 ;
;
если 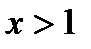 и
и  , то
, то  ;
;
если 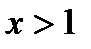 и
и  , то
, то  ;
;
если 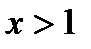 и
и  , то
, то  .
.
Полученные результаты оформим в виде таблицы (6.1.3) значений  :
:
| при |  |  |  |  |
 | ||||
 | 0,17 | 0,28 | 0,37 | |
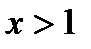 | 0,44 | 0,65 |
Для двумерной непрерывной случайной величины вводится понятие плотности вероятности
 . (6.1.4)
. (6.1.4)
Геометрическая плотность вероятности  представляет собой поверхность распределения в пространстве
представляет собой поверхность распределения в пространстве 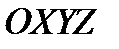 (рис. 6.1.3).
(рис. 6.1.3).
Рис. 6.1.3
Двумерная плотность вероятности обладает следующими свойствами:
1. 
2. 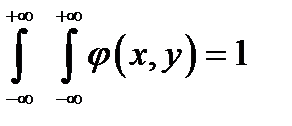
3. Функция распределения  может быть выражена через
может быть выражена через 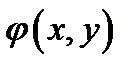 по формуле
по формуле
 . (6.1.5)
. (6.1.5)
4. Вероятность попадания непрерывной случайной величины  в область
в область  равна
равна
 . (6.1.6)
. (6.1.6)
5. В соответствии со свойством (4) функции  имеют место формулы:
имеют место формулы:
 (6.1.7)
(6.1.7)
 (6.1.7)
(6.1.7)
 (6.1.8)
(6.1.8)
 (6.1.9)
(6.1.9)
Пример 6.1.4. Задана функция распределения двумерной случайной величины
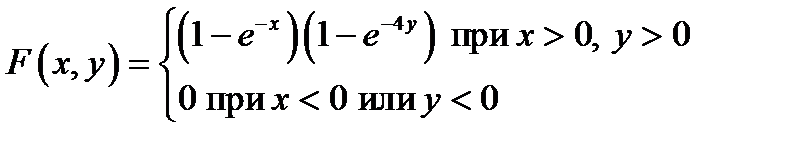 .
.
Найти: 1) двумерную плотность вероятности  ; 2) вероятность попадания случайной величины
; 2) вероятность попадания случайной величины  в прямоугольник, ограниченный прямыми
в прямоугольник, ограниченный прямыми  ,
,  ,
,  ,
,  .
.
Решение. 1) Так как  , то дифференцируя
, то дифференцируя  сначала по
сначала по 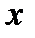 :
:  , а затем по
, а затем по 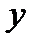 :
:  , получим
, получим
 .
.
2) Используя формулу (6.1.3) и рис. 6.1.4, получим 





 .
.
y
(0,1) (4,1)
(0,0) (4,0) х
Рис. 6.1.4.
По аналогии с условными вероятностями вводятся условные законы распределения составляющих непрерывной двумерной случайной величины 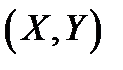 , а именно
, а именно
 - (6.1.10) условная плотность распределения Х при заданном значении
- (6.1.10) условная плотность распределения Х при заданном значении  ;
;
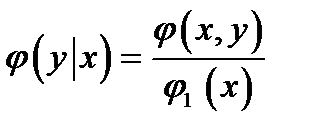 - (6.1.11) условная плотность распределения Y при заданном значении
- (6.1.11) условная плотность распределения Y при заданном значении  .
.
Если случайные величины X и Y независимые, т.е. закон распределения каждой из них не зависит от того, какое значение принимает вторая величина, то условные и безусловные законы Х и Y совпадают. В частности,  и
и  . Таким образом, для независимых составляющих Х и Y двумерная плотность вероятности находится следующим образом
. Таким образом, для независимых составляющих Х и Y двумерная плотность вероятности находится следующим образом
 (6.1.12) и функция распределения
(6.1.12) и функция распределения  имеет вид
имеет вид
 . (6.1.13)
. (6.1.13)
Заметим, что если имеют место соотношения (6.1.12) или (6.1.13), то составляющие Х и Y – независимые случайные величины.
Если составляющие Х и Y дискретной случайной величины – независимые случайные величины, то
 , (6.1.14) где
, (6.1.14) где 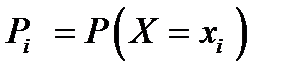 ,
,  ,
, 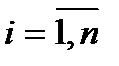 ,
,  .
.
Пример 6.1.5. Законы плотности распределения независимых составляющих Х и Y:



Найти: 1) плотность совместного распределения; 2) функцию распределения системы 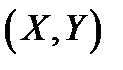 .
.
Решение. 1) В силу независимости составляющих Х и Y плотность совместного распределения
 при
при  и
и
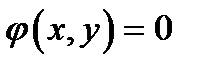 при
при  или
или 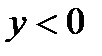 .
.
2) Найдем  и
и  .
.

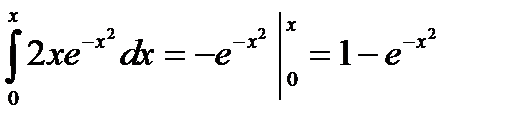 .
.
Аналогично  .
.
Тогда  при
при  ,
,  ,
,
 при
при  или
или  .
.
 2017-12-14
2017-12-14 3256
3256