Теоретические предпосылки разработки электрохимической газоочистной установки

Основная идея, заложенная в предлагаемых нами новых электрохимических установках серии В (В0–В9) основана на известных природных процессах — явлениях самоэлектроочистки и вообще униполярной ионной активности биосферы. Прототипом данных установок являются известные всем люстры Чижевского. Обратим внимание на широкую распространенность и даже насыщенность флоры острыми краями листьев, иголок хвои, травинок и т.д.

Вторым важным при этом природным фактором, ответственным на наш взгляд, за очистку атмосферы от примесей, служит вода, находящаяся в атмосфере в виде паров, аэрозолей, дождевых капель и т.д.

Разработанный нами принцип аэроионной очистки технологических газов базируется на вышеизложенных наблюдениях и фактах. Принципиальная схема для его реализации изображена на рисунке 2.5.

Потоки Q ₁ и Q ₂, в зависимости от конкретной реализации установки, могут иметь сложную геометрию (см. ниже).

 

Рис. 2.5. Принципиальная схема очистки технологических газов: К — катод; J — остроконечные иглы на поверхности катода, направленные острием к аноду; А — анод в виде спокойной поверхности текущей воды; Q ₁ — поток атмосферного воздуха; Q ₂ — поток подвергаемого очистке газа; Q ₃ — дополнительный поток воздуха; Z — активная зона; Р — диэлектрическая подложка анода; W — слой воды

При расстоянии между остриями игл и анодом около десятков сантиметров и потенциале катода порядка 10⁵ В, создается электрическое поле высокой напряженности и в активной зоне возникает темновой разряд, который характеризуется отсутствием свечения в основном объёме и прилегающем к аноду пространстве.

Пространство от острий игл до подложки анода, по отношению к протекающим процессам в качественном отношении, может быть разбито на четыре основных участка: Z ₁, Z ₂и Z ₃ — в газовой среде и W — в потоке воды (рис. 2.5). На участке Z ₁ активными областями являются окрестности острий игл, где напряженность электрического поля достигает ≥ 10¹¹В/м.

Определяющим характер протекающих процессов на участке Z ₁ является огромное электрическое поле напряженностью порядка 10¹¹ В/м. Это приводит к интенсивной вторичной эмиссии ионов, вследствие электронных ударов по нейтральным молекулам, с рождением положительного иона и одного или нескольких электронов, к столкновениям разогнанных электрическим полем положительных ионов с нейтральными молекулами. Источником первичных (затравочных) электронов служит автоэлектронная эмиссия из металла игл и естественная ионизация газа.

Вне области Z ₁ вторичная эмиссия практически отсутствует, и по отношению к области Z ₂ область Z ₁является источником электронов и возбужденных, в предыдущих столкновениях, молекул. Высокая энергия электронов в области Z ₁ведет к образованию потока атомов — осколков молекул.

Таким образом, область Z ₁является для области Z ₂источником газа обогащенного атомарными компонентами, свободными радикалами, возбужденными молекулами и электронами.

На условной границе области Z ₁, т.е. на расстоянии от острия иглы порядка h ₁ = 2·10^–4 м,скорость дрейфа отрицательных ионов достигает 500 м/с (например кислорода при их подвижности около 2 м/см·В):

, (2.1)

v = 2·0,25·10^–5 = 0,5·10⁵ cм/с = 500 м/с,(2.2)

что превышает скорость звука и ведет к образованию ударной волны.

Внутри же области Z ₁ скорость дрейфа ионов значительно выше. Поскольку подвижность электронов значительно выше подвижности положительных ионов, в области Z ₁ образуется избыток положительного объемного заряда, что с одной стороны, экранирует поле иглы, а с другой — вследствие инерционности этих процессов, вызывает высокочастотные колебания напряженности электрического поля в области Z ₁ и величины объемного заряда в ней. Ионный дрейф с большой скоростью (37) вызывает соответствующие конвективные потоки газа, показанные на рисунке 2.6 [158].

 

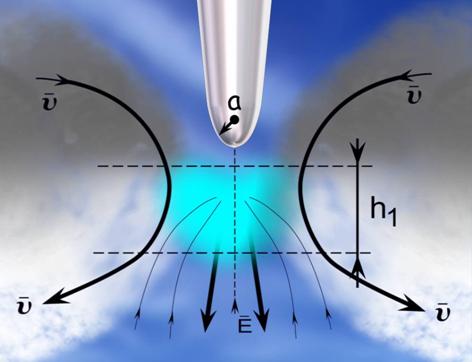
Рис. 2.6. Физические процессы в области острия иглы: — электрическое поле, υ _1, υ ₂ — поток газа, r_u — радиус кривизны острия иглы, h ₁ — размер области вторичной эмиссии

Для восполнения дефицита массы в области Z ₁, вызванного конвективными исходящими из Z ₁, потоками (рис. 2.6), возникает входящий из области Z ₂ в область Z ₁ поток . При этом и обеспечивают интенсивный массообмен между областями Z ₁ и Z ₂. На фоне (2.2) можно отметить, что скорость прокачки газа (поток Q ₂ на рисунке 2.5) составляет несколько единиц метров в секунду.

В области Z ₃поверхность воды находится в поле катода. Таким образом, область Z ₂, через которую прокачивается подвергаемый воздействию (очистке) газ с одной стороны обогащается продуктами области Z ₁, с другой — протонным потоком из области Z ₃.

Продукты химических реакций и физических процессов в области Z ₂, приобретая отрицательный заряд, попадают на поверхность анода и уносятся водой. В области W (рис. 2.5) — в потоке воды происходят обычные электрохимические процессы, при этом катодом служит поверхность воды, обращенная к катоду, а анодом — заземленный сток или исток.

Поток воздуха Q ₂создает воздушную подушку между загрязненным воздухом и иглами, это исключает попадание крупных пылевых и аэрозольных частиц на поверхность игл. В то же время, молекулярные компоненты потока Q ₂ циркулируют между областями Z ₁и Z ₂(потоки υ₁, υ₂). Это же относится и к аэрозольным частицам околомолекулярных размеров. Попадающие в область Z ₂пылевидные частицы и капельки аэрозолей облучаются мощным отрицательно ионизированным потоком и относятся электрическим полем к аноду, попадая на который, они уносятся к стоку.

Из всего вышесказанного следует, что источники возбуждения попавших в зону реакции частиц, различны [17, 36].

Численный расчет электрического поля описанного катода весьма трудоемок, специфичен для каждого набора размеров, и фактически, может рассматриваться как эксперимент. При таком расчете качественная картина проявляется как интерпретация результатов конкретных расчетов и далеко не всегда прозрачна.

Основным рабочим элементом катода являются острия игл, у поверхности которых создается высокая напряженность электрического поля. Несмотря на то, что окрестность острия находится в поле соседних игл, на расстояниях от острия порядка радиуса его кривизны h ~ r _u, влияние соседних игл и анода пренебрежимо мало.

Действительно, если F — потенциал катода, z — расстояние между иглами, Н — расстояние до поверхности анода, то напряженность поля на расстоянии h от данной иглы составит:

E ₁ = – (2.3)

(Как обычно в таких случаях, мы заменяем острие шариком с его радиусом).

Поле острия соседней иглы:

E ₂ = – (2.4)

Поле зеркального заряда (для плоского анода):

E ₃ = (2.5)

Для реальных значений:

F = 10⁵B,

r_u = 10^–6м,

z = 35·10^–3м,

Н = 0,15 м

получим:

, (2.6)

. (2.7)

Для сравнения, на расстоянии h = r _u поле длинной иглы составит:

. (2.8)

Даже если учесть поле всех игл и считать, что они не распределены на инжекторе, а сосредоточены на расстоянии z от данной иглы (то есть значительно усиливаем оценку), то при числе игл N = 10⁴ поле острий и их отражений не превзойдет в окрестности данного острия величины:

2 N (2.9)

очевидно:

1,6·10⁶ ‹‹ 10¹¹

Таким образом, в непосредственной окрестности острия электрическое поле определяется исключительно острием [158].

Оценим расстояние от острия h ₁, на котором начинают сказываться поля соседних игл:

, (2.10)

откуда

. (2.11)

Исходя из длины свободного пробега электрона можно получить для зависимости энергии столкновения электрона с атомами и молекулами W от расстояния до иглы h:

. (2.12)

В непосредственной близости от острия:

(2.13)

В тоже время от расстояния h ₂, соответствующим энергии 10 эВ:

(2.14)

Для h ₃, соответствующего 0,5 эВ:

, (2.15)

происходят наиболее значимые электрохимические процессы возбуждения электронов в атомах и молекулах, положительная ионизация, возбуждение колебательных и вращательных движений. На меньших чем h ₂ расстояниях происходит лавинная ионизация практически каждым свободным электроном.

Качественную картину электрического поля можно точно определить для плоских катода и анода следующим образом [158]. Пусть иглы расположены на катоде в квадратных ячейках с шагом h, расстояние от плоскости, проходящей через острия игл до анода — H, радиус кривизны острий — r _u.

Введем декартову прямоугольную систему координат, начало которой совпадает с центром одного из острий, ось z направлена перпендикулярно к аноду, оси x и y проходят через центры острий ближайших игл (рис. 2.7).

 

Рис. 2.7. Схема расположения декартовой прямоугольной системы координат по отношению к аноду, катоду и центрам игл

Пусть , , 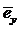— соответствующие индексам координатные единичные векторы. Пусть — произвольный вектор (радиус-вектор точки в пространстве между остриями игл катода и анодом).

Тогда

— (2.16)

радиус-вектор острия с номером m по координате x по счету от начала координат, и с номером n — соответственно по x. При этом для бесконечной плоскости:

Для конечной плоскости Причем ; (понятно, что m, n, M ₁, M ₂, N ₁, N ₂ — целые числа).

Тогда

— (2.17)

радиус-вектор зеркального заряда с номерами m и n.

Тогда при отрицательном потенциале катода F потенциал в точке , создаваемый данным острием и его зеркальным зарядом будет иметь вид:

. (2.18)

Потенциал в точке от всех острий для конечной плоскости будет тогда иметь вид:

, (2.19)

a напряженность электрического поля в точке будет:

, (2.20)

то есть

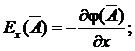(2.21)

(2.22)

(2.23)

Модуль напряженности поля Е, очевидно будет:

(2.24)

Если решетка игл смещена (но не повернута) на вектор :

, (2.25)

то векторы и будут иметь вид:

; (2.26)

. (2.27)

Наконец, если решетка игл представляет собой сумму К таких решеток с шагами h_xj, h_yj — разными по осям x и y, подставляя (2.26) и (2.27) в (2.19) и производя дифференцирование в соответствии с (2.21), (2.22) и (2.23), получим для величины напряженности электрического поля следующие уравнения:

(2.28)

(2.29)

(2.30)

(2.31)

(2.32)

К — число решеток.

Для используемых нами F = 10⁵ В; r _u = 10^–6 м; Н = 25·10^–2 м характерных значениях:

(2.33)

поле по формулам (2.28), (2.29), (2.30) и (2.24) рассчитано и представлено на рисунках 2.8–2.10.

Рис. 2.8. Зависимость модуля напряженности электрического поля в средней части рабочего промежутка от шага игл квадратной решетки h

 

Рис. 2.9. Зависимость модуля напряженности электрического поля E от Z при различных расстояниях x от оси иглы

Рис. 2.10. Зависимость нормальной к аноду составляющей напряженности электрического поля E _z от расстояния до катода z при различных смещениях x относительно оси иглы

На рисунке 2.8 представлена зависимость модуля напряженности электрического поля на горизонтальном участке в зависимости от шага h квадратной ортогональной решетки игл.

При конической форме катода и анода картина поля в окрестности катода принципиально не меняется, а на протяжении оси иглы к аноду, вместо практически горизонтального участка, возникает снижение напряженности.

На расстояниях менее 0,5 см от острия поле определяется исключительно острием и имеет зависимость ~ r^{– 2}, где r — расстояние до острия.

Из рисунков 2.8–2.10 также следует, что на расстояниях L от игл в сторону анода более L = 2,5 см поле однородно и составляет Е ≈ 1050 В/м.

Для определения плотности ионов в этой области будем считать, что начало координат оси z находится на этом расстоянии от игл и ось z направлена в сторону анода.

Пусть Е ₀ — напряженность поля, создаваемая катодом в этом начале координат. Величинами Е_х и Е_y пренебрежем ввиду их малости. Тогда поле объемного заряда и его зеркального изображения относительно анода будет:

, (2.34)

где n (z) — плотность ионов; e — заряд электрона; ε₀ — диэлектрическая проницаемость вакуума; ε ≈ 1 — диэлектрическая проницаемость газа. Если I — плотность ионного тока, k — подвижность ионов, то

. (2.35)

В силу сохранения заряда в стационарном режиме:

(2.36)

дифференцированием по z (2.35) приводится к виду:

(2.37)

интегрируя (2.37), получим:

,

В — постоянная интегрирования. Поскольку при z = 0

,

то:

. (2.38)

Тогда суммарная (от игл и объемного заряда) напряженность поля составит

.

При общем токе катода 0,05 А, расстоянии между иглами квадратной решетки h = 3,5 см, числе игл N = 10⁴, получим

A/м², (2.39)

если k = 2·10^–4 м²/сек·В, то

. (2.40)

Так, при z = H – L = 0,225 м:

, (2.41)

поскольку E ₀ ~ 10³В/м,в (2.41) ею можно пренебречь, тогда получим

. (2.42)

Плотность ионов при z = 0:

(2.43)

при E ₀ = 10³, получим:

. (2.44)

Зависимость E (z) (2.41) на рисунке 2.11.

Из (2.38) с учетом (2.43), зависимость n (z)имеет вид:

. (2.45)

Зависимость (2.45) — на рисунке 2.12.

 

Рис. 2.11. Напряженность электрического поля в рабочей зоне установки с учетом поля объемного заряда

 

Рис. 2.12. Плотность отрицательных ионов в рабочей зоне при различных напряженностях электрического поля E ₀ на границе прикатодной области

Данные картины поля, приведенные на рисунках 2.8–2.12, были положены в основу инженерных расчетов установки.

 

 

2.3. Инициирование химических реакций
в активной зоне темнового электрического разряда
в системе игольчатый электрод–газ–жидкость

Как описано выше, в разрабатываемых нами газоразрядных установках серии В0–В9 между инжектором (игольчатыми электродами) и жидким анодом имеется активная реакционная зона, которая является полем высоких энергий. Под действием электрического разряда в этой зоне при прохождении газовой смеси происходит ряд физических и химических процессов.

Как известно [64–68, 78], специфические особенности протекания электрохимических реакций под действием электрического разряда обусловлены тем, что в отличие от традиционных химических процессов они проводятся в системах открытых в термодинамическом смысле: для получения такого состояния (состояние плазмы) необходимы внешние источники энергии и часть её расходуется на осуществление (инициирование) химических процессов. Это же объясняет и существенную неравновесность, наблюдаемую и используемую во многих плазмохимических процессах.

Можно выделить три основных этапа в инициировании и осуществлении электрохимических реакций в данных условиях. Во-первых, энергия от внешнего источника передается в газовую среду через электронную компоненту системы. Во-вторых, электронный газ передает полученную энергию тяжелым частицам в процессах нагрева, возбуждения внутренних степеней свободы атомов и молекул, ионизации, диссоциации. Таким образом, происходит перераспределение энергии внешнего источника между тяжелыми частицами, и создаются химически активные частицы. Обычно, доля, идущая на нагрев газа (особенно в неравновесных условиях) мала, и в основном, энергия электронов расходуется на возбуждение внутренних степеней свободы атомов и молекул.

В-третьих, происходят химические превращения в полученной электрохимически активной среде. Таким образом, процессы в химически активной плазме связаны с присутствием трех групп частиц: заряженных, возбужденных и нейтрально возбужденных (исходные молекулы, атомы, радикалы, продукты промежуточных реакций), и роль электронной эмиссии в инициировании реакций является определяющей.

Следует отметить, что активная газоразрядная зона (зона плазмы) характеризуется большой плотностью энергии, а присутствие большого числа реакционно-способных частиц ведет к многоканальности химических процессов в этих условиях [41–43]. Это означает, что один и тот же суммарный процесс в зависимости от параметров плазмы (давление, степень ионизации, удельный энерговклад и т.д.) может происходить принципиально различными путями. Применительно к задачам это проявляется в необходимости поиска механизмов, идущих с большой эффективностью, а также условий, в которых эти механизмы реализуются.

Классическая (равновесная) химическая кинетика оперирует понятием константы скорости химической реакции, определяемой уравнением Аррениуса [68, 78]:

k = A (T)exp(– E_a / kT),

где Е_а — характерная величина энергетического барьера реакции (энергия активации), Т — температура системы. Это выражение справедливо для термодинамически равновесных условий (сохранение равновесных условий при протекании химической реакции), для адиабатических (медленных) столкновений и возможности рассмотрения соударений молекул в модели твердых шаров. Невыполнение хотя бы одного из этих условий, а как следует из проведенного выше рассмотрения (в условиях плазмы это так), ведет к невозможности использования этого выражения для описания химических реакций в активной газоразрядной зоне (плазме).

В плазме характерные времена различных химических и физических процессов сближаются и, поэтому, их нельзя рассматривать независимо, как это делается в классической химической кинетике. Из этого следует, что при рассмотрении химических процессов в плазме нельзя пользоваться только химическими представлениями, равно как и при анализе физических процессов нельзя не рассматривать химические явления. Так, химическая активность плазмы во многом определяется процессом передачи энергии от внешнего источника на внутренние степени свободы тяжелых частиц, который зависит от характеристик электронной компоненты плазмы, а именно, функции распределения электронов по энергиям (ФРЭЭ) и их концентрации. Эти характеристики определяют, например, скорость образования атомов и радикалов и, соответственно, скорость образования продуктов [60, 69, 78].

С другой стороны, ФРЭЭ зависит от напряженности электрического поля в плазме и каналов потерь энергии электронами в столкновениях с тяжелыми частицами. Последние зависят от состава плазмы. Напряженность электрического поля в ионизированной газовой среде самостоятельных разрядов определяется уравнением баланса заряженных частиц, т.е. вновь химическим составом газовой среды через механизм ионизации и ионный состав плазмы [60–75]. Из этого видно, что физические и химические явления самосогласованны, т.е. изменение любого из параметров плазмы (в число которых включены и химические характеристики) ведет к изменению остальных.

Роль возбужденных частиц в протекании физико-химиче­ских процессов в ионизированной системе может быть продемонстрирована на примере процессов, стимулированных колебательным возбуждением. В неравновесной плазме ряда молекулярных газов (N₂, CO, CO₂ и др.) до 95 % энерговклада в плазму может быть сосредоточено в колебательных степенях свободы молекул в основном электронном состоянии [54, 66]. С учетом колебательного возбуждения и соответствующей колебательной энергии Е_v, константа скорости реакции с участием колебательно возбужденных молекул может быть представлена в виде:

, (2.46)

где k ₀ — предэкспоненциальный множитель константы скорости, α — коэффициент использования колебательной энергии. Для эндотермических реакций α = 0,9–1, для экзотермических α = 0,1–0,3, для термонейтральных α = 0,3–0,5 (для реакций с образованием промежуточного комплекса) и порядка 0,01 для реакций без образования комплекса [54, 66]. Отсюда следует, что для колебательно возбужденных молекул с энергией Е_v, активационный барьер как бы снижается на величину α Е_v.

Колебательно-поступательная неравновесность приводит к усилению звуковых волн в ионизированной газовой системе (плазме). Неравновесная химическая реакция может оказывать стабилизирующее действие на развитие ионизационно-перегрев­ной неустойчивости, что связано с тем, что колебательная энергия молекул может расходоваться в химических реакциях и лишь в незначительной степени переходить в нагрев газа.

Механизм ионизации в самостоятельных электрических разрядах и, соответственно, напряженность электрического поля в плазме, зависят от присутствия газовых добавок иих химической природы. Добавки, оказывающие влияние на механизм ионизации могут появиться в плазме в результате химических превращений исходных реагентов. В случае прямой ионизации, появление легко ионизуемой добавки ведет к уменьшению напряженности электрического поля, тогда как в случае ступенчатой ионизации, возможно как увеличение, так и уменьшение напряженности электрического поля. Если возможен процесс пеннинговской ионизации молекул добавки возбужденными частицами, участвующими в ионизации, то напряженность поля уменьшается [60–68].

Если же молекулы добавки участвуют в процессе тушения возбужденных частиц без ионизации, напряженность поля увеличивается. Эти процессы демонстрируются обычно в смесях инертных газов с различными добавками, и эффект зависит как от инертного газа, так и от добавки. Эти явления используются, например, в аналитической химии, и применение гелия в качестве основного газа позволяет ионизовать любую примесь (первый потенциал возбуждения гелия НЕ превышает потенциалы ионизации почти всех молекул).

Влияние на напряженность поля может оказать и изменение ионного состава плазмы. Например, введение углеводородов в водородную плазму приводит к замене основного иона с Н₃⁺ на тяжелые углеводородные ионы, что ведет к уменьшению скорости диффузионной гибели заряженных частиц [69, 78]. Ясно, что степень влияния химических процессов на те или иные характеристики плазмы зависит от механизмов плазмохимических процессов.

Так как элементарным актом плазмохимической реакции является процесс, происходящий с данной молекулой в данном энергетическом состоянии, то его характеристикой является уровневый коэффициент скорости элементарной реакции k_i:

, (2.47)

где σ _i (ε) — сечение реакции с молекулой в i -том энергетическом состоянии; f  (ε) — функция распределения частиц по энергиям; ε — энергия частицы, ε _пор — пороговая энергия процесса. Суммарный коэффициент скорости химической реакции

(2.48)

где α _i — относительные заселенности соответствующих квантовых уровней.

Отсюда следует, что для анализа химических реакций в ионизированной зоне (плазме), необходимо знать заселенности частиц по внутренним степеням свободы, сечения процессов и функции распределения частиц. Константа скорости традиционной химической кинетики лишь в частных случаях может совпадать с k Σ.

Таким образом, подводя итоги выше изложенного, можно сделать следующие выводы:

1. Реакции под действием электрического разряда можно рассматривать как двухступенчатый процесс, в котором первой стадией является образование химически активных частиц и их реакции между собой, а вторая стадия — реакции активных частиц с другими веществами. Например, электроны сталкиваются с молекулами газа и возбуждают их. Возбужденные прямым электронным ударом молекулы могут диссоциировать или инициировать другие химические реакции [43–45]:

е + М → М* + е (2.48)

R + M* → Продукты (2.49)

Здесь е — электрон; М* — атом или молекула в электронно-возбужденном состоянии, R — молекула-реагент.

2. Константы скоростей этих процессов зависят как от величины напряженности электрического поля, так и от химического состава газовой смеси. Условия разряда определяют типы активных частиц и их относительные количества. Как и для большинства химических систем, температура является основным параметром, описывающим распределение частиц по энергиям [46–49].

3. Для экспериментального изучения химических реакций в газоразрядной зоне требуется применять значительно более широкий набор методик, чем обычно используемый в электрохимии. Это такие методы исследования газовой фазы (состав нейтральной и заряженной компоненты плазмы), как оптическая спектроскопия, лазерные методы, масс-спектроскопия, хроматография, а также методы исследования дисперсной фазы и характеристик поверхности (электронная микроскопия для химического анализа, Оже и Раман-спектроскопия и др.).

 

 

2.4. Условия осуществления химических реакций
в активной зоне

А. Активные факторы на острие игольчатого электрода. В аэроионных электрохимических установках серии В0–В9, как отмечено нами выше, между инжектором (инжекторным электродом) и жидким анодом имеется активная реакционная зона, которая является полем высоких энергий. Под действием электрического разряда в этой активной зоне при прохождении газовой смеси происходит ряд физических и химических процессов.

Основные физико-химические процессы активного темнового разряда, приводящего к инициированию химических реакций, протекают на острие иглы, где имеется высокая напряженность электрического поля. Напряжение в каждом случае ограничено возможностью электрического пробоя. Ток, текущий через одну иглу по экспериментальным данным составил I = 10^–6 A, J = I / S ² = = 1 А/мм².

При расстоянии между остриями игл и анодом около десятков сантиметров и потенциале катода порядка 10⁵ В создается электрическое поле высокой напряженности, и в активной зоне возникает темновой разряд, который характеризуется отсутствием свечения в основном объёме и прилегающем к аноду пространстве.

В разрядной зоне установки активными факторами, воздействующими на химический процесс, являются:

- высокая напряженность электрического поля;

- электронная эмиссия;

- вторичная ионизация веществ;

- поляризация молекул, возбуждение молекул и атомов;

- высокая температура;

- фотоионизация;

- СВЧ-излучение (электромагнитные колебания);

- ударная волна.

Исследованию продуктов электрохимических процессов в разряде посвящен целый ряд работ [100–106]. Анализ продуктов электрохимических процессов проводился авторами вне зоны разряда методами масс-спектрометрии, газовой хроматографии и по перепаду давлений.

Эти методы дают возможность измерить только средние значения концентраций соответствующих продуктов реакции. Между тем, известно, что разряд в газоразрядной установке имеет дискретный характер, т.е. состоит из отдельных каналов, параметры которых, например, температура, концентрация электронов, концентрация возбужденных атомов и молекул и другие, — отличаются от параметров окружающего газа.

Неоднородность разряда должна учитываться при изучении механизма электрохимических процессов в газоразрядных установках. Между тем, до сих пор свойства газа усреднялись по всему объему. Спектральные исследования могли бы дать сведения о процессах, протекающих во всех каналах разряда.

Спектры испускания в темновом электрическом разряде ранее не были исследованы, поэтому нами были сделаны попытки изучения реальной картины процессов на острие иглы в электрическом поле высокой напряженности.

С этой целью нами была разработана оптическая установка, предназначенная для исследования характера свечения острия иглы в газовой среде (см. раздел 3).

а) выдержка — 20 с, увеличение — ´20 (без напряжения с подсветкой). Опорная микрофотография острия (сделана для определения фронтальной плоскости области излучения и кривизны острия)

б) выдержка — 12,5 мин., увеличение — ´20, напряжение — 20 кВ, ток — 20 мкА

Рис. 2.13. Спектр испускания на острие иглы

Спектры излучения в темновом электрическом разряде нами изучены в широком интервале длин волн, в зависимости от давления, силы тока и скорости потока газа. Данные спектроскопического исследования были сопоставлены с результатами, полученными при анализе продуктов вне зоны разряда.

На данном снимке (рис. 2.13 б) явно различимы две области:

1. Область белого свечения имеет четко очерченные границы и размеры 40´40 мкм. Это область самостоятельного разряда; излучение обусловлено ионизацией и деионизацией, главным образом, молекул азота.

2. Область голубого свечения с яркостью свечения обратно пропорциональной квадрату расстояния от центра иглы. Свечение обусловлено двумя факторами: синхротронным излучением ионов, движущихся в области высокой напряженности и градиента напряженности электрического поля и излучением при столкновениях ионов.

Б. Рассмотрим основные требования к разряду, предназначенному для инициирования химических реакций в газовой среде.

Пусть в объеме газа генерируются активные радикалы R·, а в газовой среде имеется вещество М, взаимодействие которого с радикалами R· нас интересует. Тогда скорость взаимодействия вещества М с радикалами будет определяться соотношением:

W ₁ = Ak ₁[M][R·],

где k ₁ — константа скорости реакции; А — кинетический фактор, характеризующий взаимодействия частиц; [M] — концентрация вещества в газовой зоне; [R·] — концентрация радикалов в газовой фазе.

Радикалы R·, образующиеся в газовой фазе, могут также расходоваться при взаимодействиях между собой, образуя неактивные продукты, со скоростью W ₂ = k ₂[R·]². Чтобы не допустить значительной потери активных частиц, необходимо выполнить условие W ₂ << W ₁, или:

(условие I).

Таким образом, для того чтобы активные радикалы расходовались в основном на взаимодействие с веществами, содержащимися в составе газовой смеси, их концентрация должна зависеть от концентрации компонентов газа и быть достаточно малой.

Согласно оценкам А.В.Гришина [159], плотность ионов, одновременно находящихся в рабочей области установки В5, составляет δ = 10¹⁵ м^–3, т.е. количество ионов, одновременно находящихся в рабочей области, составляет:

N_u = Z_u ^. W (L) = 10^15. 2,021 = 2,021·10¹⁵.

По этим расчетным данным [159], при расходах газового потока Q 0,25 и 3,75 м³/с в расчете на 1 молекулу проходящего через рабочую область газа, количество элементарных зарядов, прошедшее через газ составит:

;

.

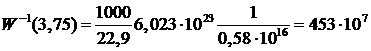Такая плотность частиц характерна для слабоионизированной плазмы, коронного или слаботочного искрового разряда (ток ~ 1 мА), либо, возникающего под действием пучка электронов с плотностью тока ~ 0,1 мА/см². Здесь важно подчеркнуть, что при сильном увеличении тока разряда будет генерироваться слишком много активных частиц, и эффективность реакции будет падать, а энергозатраты на её осуществление — увеличиваться.

В. Теперь рассмотрим требования к объему газовой фазы и форме полости с газом.

Пусть в объеме газа при электрическом разряде образуется в единицу времени 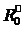радикалов. Их концентрация будет 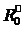/ V_r, где V_r — объем газа.

Гибель радикалов будет происходить со скоростью k ₂(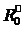 / V_r)², а расходование на реакции с компонентами газовой фазы со скоростью

Ak ₁[M](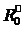 / V_r).

Тогда приведенное выше нами условие

примет следующий вид:

(условие II).

Отсюда следует, что при определенной скорости образования активных радикалов, всегда можно выбрать такой маленький объем газовой фазы, когда условие (II) не может быть выполнено, и образующиеся радикалы будут погибать преимущественно при взаимодействиях между собой, т.е. объем газовой полости должен быть не слишком малым, и в конкретных случаях может возникать необходимость его увеличения.

Если частицы будут гибнуть на стенках (это относится в первую очередь к частицам в возбужденных состояниях), доля погибших частиц для случая газового объема в форме цилиндра с радиусом r и высотой h будет:

.

Таким образом, из этих данных следует, что объем полости при необходимости следует увеличивать за счет радиуса, оставляя минимальной её высоту.