Частотные характеристики. Частотные характеристики отражают зависимости амплитуды и фазы от частоты синусоидальных колебаний при прохождении этих колебаний через звено или систему

 

Частотные характеристики отражают зависимости амплитуды и фазы от частоты синусоидальных колебаний при прохождении этих колебаний через звено или систему.

В отличие от рассмотренного воздействия в виде единичной функции, для построения частотных характеристик на вход звена подают периодически изменяющиеся входные воздействия.

Изменение амплитуды и фазы синусоидального колебания при прохождении его через элементы системы регулирования зависит только от частоты ω этих колебаний.

Хотя частотные характеристики дают зависимости амплитуд и фаз от частоты ω в установившемся режиме работы системы, тем не менее их называют динамическими, так как они позволяют определять устойчивость системы в динамическом, то есть переходном ре­жиме.

Пусть на входе звена действует сигнала х = a sin ωt. Тогда на его выходе устанавливаются синусоидальные колебания с другой амплитудой и сдвинутые по фале на угол φ: y = b sin (ωt – φ).

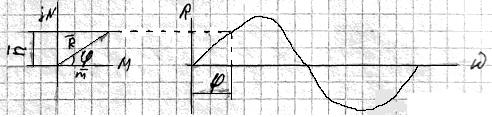
a – условное обозначение звена;

б – ампли­тудно-частотная; в – фазо-частотная

Рисунок – Частотные характеристики звена

 

 

Различают амплитудно-частотные и фазо-частотные характери­стики.

Амплитудно-частотная характеристика (рис. б) – это зависимость амплитуды колебаний на выходе от частоты колебаний на входе элемента или всей АСУ:

.

 

Фазо-частотной характеристикой (рис. в) называют зависимость разности фаз между входными и выходными колеба­ниями от частоты колебаний:

.

 

В теории автоматического регулирования используется совмещенная амплитудно-фазо-частотная характеристика (АФЧХ), которая выражает соотношение между амплитудами выходною и входного колебаний и сдвигом фаз в зависимости от частоты. Другими словами, это есть отношение вектора колебания выходной величины к вектору колебания входной. Так, если х = aе ^jωt – вектор колебаний входной величины, а у = bе ^jωt–φ – век­тор колебаний выходной, то амплитудно-фазовая характеристика звена

Таким образом, амплитудно-фазо-частотная характеристика яв­ляется векторной величиной. на плоскости комплексного перемен­ного она изображается кривой, которая называется годографом век­тора W (jω) при наименьшем ω от –∞ до +∞.

Если входное воздействие изменяется по закону

Например, уравнение (1) из операторной формы можно привести к виду

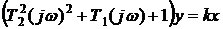
Отсюда получим АФЧХ:

(2)

В общем случае амплитудно-фазо-частотная характеристика со­стоит из вещественной R (ω) и мнимой j I (ω) частей частотной харак­теристики:

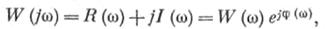
– модуль функции W (jω);

– фаза или аргумент функции W (jω).

Величина W (ω) определяет изменение амплитуды, а φ (ω) – изменение фазы колебаний на выходе звена по отношению к колеба­ниям на входе, происходящим с частотой ω.

Для выражения (2)

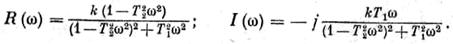
Из последних выражений следует, что вектор амшштудно-фазо-частотной характеристики W (jω) = k при ω = 0 и W (jω) = 0 при ω = ∞. В процессе изменения угловой частоты в пределах 0 ≤ ω ≤ +∞ вектор W (jω) поворачивается по часовой стрелке и описывает годограф, который охватывает п – т = 2 – 0 = 1 квадрант (здесь п и т соответственно показатели полино­мов при у и х исходного уравнения).

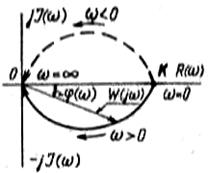
Рисунок – Амплитудно-фазо-частотная характеристика.

 

При изменении угловой частоты в пределах 0 ≤ ω ≤ –∞ годо­граф (пунктирная кривая) зеркально отображает относительно оси абсцисс годограф, построенный для 0 ≤ ω ≤ +∞

 

Для облегчения расчетов и лучшей на­глядности был предложен метод логарифмических частотных характеристик, который в ряде случаев позволяет трудоемкие расчеты заменить гра­фическими построениями при помощи номограмм и специальных шаблонов.

Логарифмическая амплитудно-частотная и фазо-частотная характеристики отличаются от характеристик, приведенных на рисунке только логарифмическим масштабом. По оси абсцисс вместо величины ω откладывают величину lg ω в логарифмических единицах (декадах [в 10 раз] или октавах [в 2 раза]), а по оси ординат при построении амнлитудно-частотных характеристик вместо величины 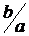откладывают величину 20 lg 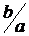, единица измерения которой называется децибелом (дБ). Это позволяет в наглядной форме строить и сравнивать частотные харак­теристики в широких пределах изменения угловой частоты ω.

Амплитудно-фазная характеристика – это зависимость одновременно амплитуды и фазы от частоты колебаний входной величины.

Частотные характеристики имеют большое значение для анализа динамических качеств АСУ.

Если на вход системы подать гармоническое воздействие (возмущение) непрерывно изменяющееся по синусоидальному (sin) закону,

х = Asin ω ₁ t,

где А – амплитудные колебания входной воздействия,

ω – угловая частота колебаний [1/с],

ω = 2 π f = 2 π (1/T); T = 2 π / ω

то если звено или система линейная на выходе также устанавливаются синусоидальное (sin) колебание, выходного параметра “у“ с той же частотой ω, но с другой амплитудой “ а ₁“.

у = а sin (ωt – φ₁) – на выходе

а ₁ < а ₂

и колебания отстающие по фазе от колебаний входного параметра на величину φ₁ (сдвиг по фазе на величину φ₁).

Увеличим частоту колебаний входного параметра, до величины ω₂ > ω₁

х = Asin ω ₁ t,

у = а ₂ sin (ω₂t – φ₂)

а ₂ < а ₁,

φ₂ > φ₁

На выходе звена устанавливается колебания с частотой ω₂, но с меньшей амплитудой а ₂ < а ₁ < А и с большим отставанием по фазе φ₂ > φ₁

 

Анализ показывает: Чем больше частота входных колебаний, тем меньше амплитуда выходных колебаний и тем больше отставание по фазе выходных колебаний по отношению к входным колебаниям.

При некоторой критической величине колебаний ω = ω_критич

 

амплитуда выходных колебаний а _критич = 0, то есть колебания на выходе звена не будут, звено или система полностью отфильтровывает поступающие ему на вход высоко частотные колебания.

 

Величина отношения амплитуды выходной величины к входной и сдвиг по фазе φ при различных частотах зависит от динамических свойств звена.

Зависимость отношения амплитуды а /А выходных колебаний к входным, от частоты ω, при изменении ω от 0 до ω_критич – называется амплитудно-частотной характеристикой.

Зависимость сдвига фазы φ от частоты ω входных колебаний, называется фазо-частотной характеристикой.

 

Кроме амплитуды и фазо-частотной характеристикой свойства звена оценивают амплитудно-фазной характеристикой, выражающей одновременное изменение амплитуды и фазы выходных колебаний, от частоты входных колебаний ω_вх.

Для получения графических изображений амплитудно-фазных характеристик звена строят на комплексной плоскости векторы длиной а для каждой частоты входных колебаний, выходящих из начала координат под углом сдвига фаз равным φ по часовой стрелке, если угол отрицательный и соединяют концы векторов плавной кривой, которая называется годографом.

годограф

 

Для аналитического определения амплитудно-фазных характеристик звена закон синусоидальных колебаний, его входных и выходных параметров выражают в векторной форме с помощью комплексных чисел на комплексной плоскости.

R = m + jn

где m – действительная часть комплексного числа;

n – мнимая часть (отрицательная часть

cosφ = m / R; sinφ = n / R R = |R| ∙(cosφ + j ∙sinφ) =|R| ∙ e ^{-j φ}

R = √(m ² + n ²)

cosφ – вещественная часть;

sinφ – мнимая часть;

e ^{-j φ} – показательная часть (единичный вектор)

e ^{-j φ} = cosφ + j ∙sinφ

входная величина х = А∙ sinωt = A e ^{–j φ}

выходная величина у = а ∙ sin(ωt–φ) = а e ^{–j (ωt–φ)} = а ∙ e ^{–j ωt}∙ e ^{j φ}

Зависимость между выходной и входной величиной звена для каждой частоты ω можно охарактеризовать отношением векторов у и х, которое представляет собой вектор W (jω) – это и есть аналитическое выражение амплитудно-фазной характеристикой в векторной форме.

На комплексной плоскости амплитудно-фазная характеристика изображается кривой, которая называется годографом вектора W (jω), при изменении частоты колебаний ω от – ∞ до + ∞.

Обычно строят положительную ветвь, когда частота колебаний ω изменяется от 0 до ∞, а отрицательную ветвь, когда частота колебаний ω изменяется от – ∞ до 0 является зеркальным отражением положительной ветви относительно действительной оси.

 

Лекция 12