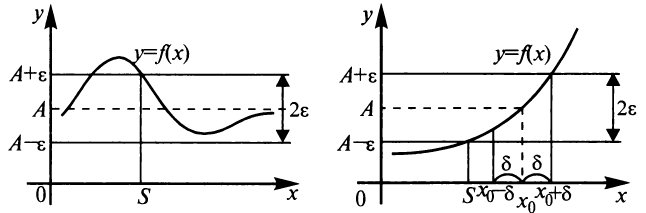
Неравенство  равносильно двойному неравенству
равносильно двойному неравенству  , соответствующему расположению части графика в полосе шириной 2ε (см. рис. 2). Аналогично неравенство
, соответствующему расположению части графика в полосе шириной 2ε (см. рис. 2). Аналогично неравенство  равносильно двойному неравенству
равносильно двойному неравенству  соответствующему попаданию точек х в δ -окрестность точки х 0.
соответствующему попаданию точек х в δ -окрестность точки х 0.
Рисунок 2 – Геометрический смысл предела функции в точке
Тема 1.3. Односторонние пределы
В определении предела функции  считается, что x стремится к х 0любым способом: оставаясь меньшим, чем х 0 (слева от х 0), большим, чем х 0(справа от х 0), или колеблясь около точки х 0.
считается, что x стремится к х 0любым способом: оставаясь меньшим, чем х 0 (слева от х 0), большим, чем х 0(справа от х 0), или колеблясь около точки х 0.
Бывают случаи, когда способ приближения аргумента х к х 0существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
Определение: Число А1 называется пределом функции у=f(x) слева в точке х 0, если для любого число ε>0 существует число d=d (ε)>0, такое, что при  , выполняется неравенство
, выполняется неравенство  .
.
Предел слева записывается так:  или f (x 0 – 0)=A1.
или f (x 0 – 0)=A1.

Аналогично определяется предел функции справа:
Определение: Число А2 называется пределом функции у=f(x) спарава в точке х 0, если для любого число ε>0 существует число d=d (ε)>0, такое, что при  , выполняется неравенство
, выполняется неравенство  .
.
Предел справа записывается так: 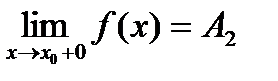 или f (x 0 + 0)=A2.
или f (x 0 + 0)=A2.

Теоремы о пределах
1. Если существуют пределы функций f (x) и g (x), то существует предел их суммы, равный сумме пределов функций f (x) и g (x)

2. Если существуют пределы функций f (x) и g (x),то существует предел их произведения, равный произведению пределов функций f (x) и g (x)

3. Если существуют пределы функций f (x) и g (x)и предел функции g (x) не равен нулю, то существует предел их отношения, равный отношению пределов функций f (x) и g (x)

Следствие:
1) 
2) 
Замечание: 
Пример1. 
Пример2. 
Пример3.  . Получили неопределенность типа 0\0. Чтобы от нее избавиться необходимо, преобразовать числитель и знаменатель выражения. Данные выражения представляют собой квадратные многочлены, поэтому, пользуясь формулой
. Получили неопределенность типа 0\0. Чтобы от нее избавиться необходимо, преобразовать числитель и знаменатель выражения. Данные выражения представляют собой квадратные многочлены, поэтому, пользуясь формулой  разложения квадратного многочлена на множители, разложим на множители числитель и знаменатель.
разложения квадратного многочлена на множители, разложим на множители числитель и знаменатель.

Замечание: При решении примеров на нахождение пределов не редко могут встретиться неопределенности вида: 
Для того, чтобы избавиться от таких неопределенностей выражение под знаком предела обычно преобразуют. Если выражение дробь, в числителе и в знаменатели которой находятся многочлены, то их раскладывают на множители. Если содержится выражение содержащее знак корня, то числитель и знаменатель домнажают на сопряженное число. Если выражение содержит разность или сумму дробей, то оно приводится к общему знаменателю.
Пример 4. Вычислить: 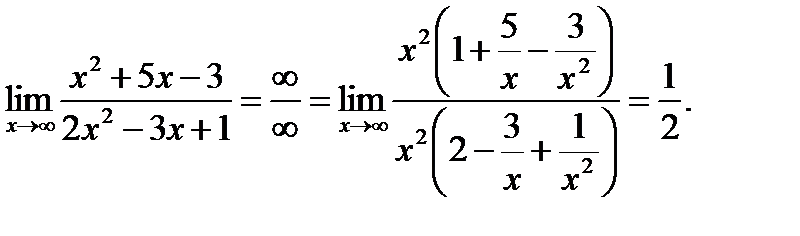
При решении воспользовались формулой 
 2017-12-14
2017-12-14 4894
4894
