Понятие определенного интеграла
Рассмотрим функцию f (x) определенную на отрезке [ a, b ].
Разобьем отрезок [ a,b ] на n элементарных отрезков точками 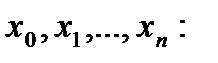
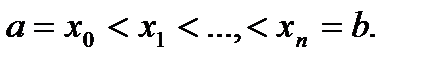
На каждом отрезке 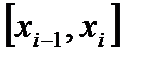 разбиения выберем некоторую точку
разбиения выберем некоторую точку 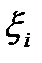 и положим
и положим 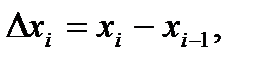 где i = 1, 2, …, n. Сумму вида
где i = 1, 2, …, n. Сумму вида
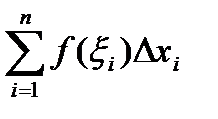
будем называть интегральной суммой для функции f (x) на отрезке [ a, b ].
Для избранного разбиения отрезка [ a, b ] на части обозначим через 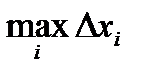 максимальную из длин отрезков
максимальную из длин отрезков 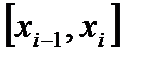 , где i = 1, 2, …, n.
, где i = 1, 2, …, n.
Определение. Пусть предел интегральной суммы при стремлении 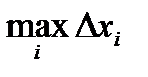 к нулю существует, конечен и не зависит от способа выбора точек
к нулю существует, конечен и не зависит от способа выбора точек 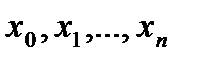 и точек
и точек 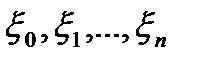 . Тогда этот предел называется определенным интегралом от функции y = f (x) на [ a, b ], обозначается
. Тогда этот предел называется определенным интегралом от функции y = f (x) на [ a, b ], обозначается  , а сама функция называется интегрируемой на отрезке [ a, b ], т.е.
, а сама функция называется интегрируемой на отрезке [ a, b ], т.е.
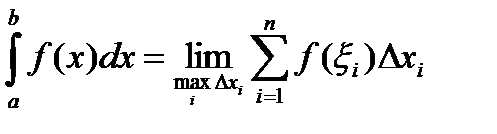 .
.
При этом число а – нижний предел, b – верхний предел; f (х) – подынтегральная функция, f (х) dx –подынтегральное выражение, а задача о нахождении 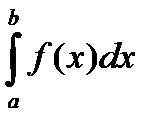 – интегрированием функции f (х) на отрезке [ a, b ].
– интегрированием функции f (х) на отрезке [ a, b ].
Свойства определенного интеграла
1. Постоянный множитель можно выносить за знак интеграла, т.е. 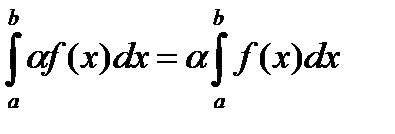
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. 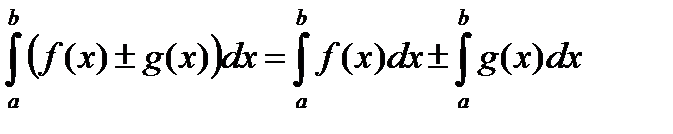
3.Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b, c.
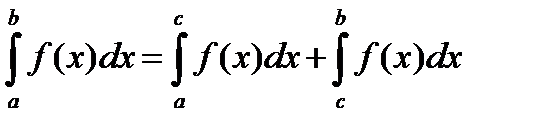
 2017-12-14
2017-12-14 757
757








