Метод замены переменной

Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый следующей формулой:

, (1)

где х = j(t) – функция, дифференцируемая на рассматриваемом промежутке. Данная формула (1) показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная замена переменной позволяет упростить исходный интеграл, а простейших случаях свести его к табличному.

Пример 4. Найти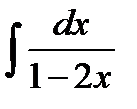

Положим t =1 – 2 х, продифференцируем обе части равенства:

(*)

Обратим внимание на то, что в данном примере выполнили замену знаменателя и осталось заменить числитель. Необходимо dx выразить через dt. Из равенства (*) следует: .

При решении воспользовались 3 табличным интегралом. После вычисления интеграла, вернулись к прежним обозначениям.

Пример5. Найти

При решении, воспользовались 6 табличным интегралом и перешли к прежним обозначениям.

Пример 6. Найти интегралы а) б)

В данных интегралах выполняем замену подкоренного выражения.

а)

б)

Пример 7. Вычислить: .

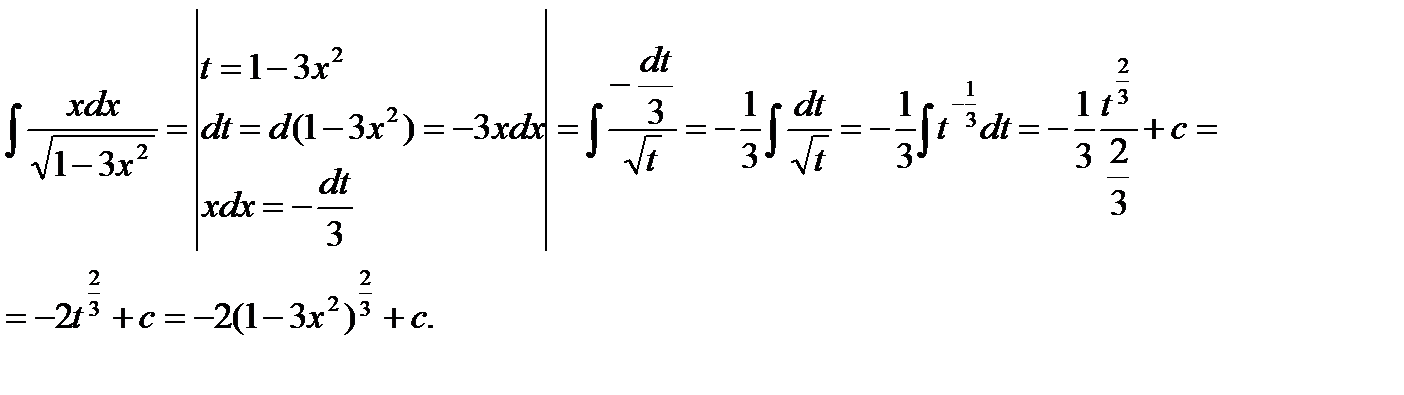
Пример8. Найти а) ; б) ; в) .

а)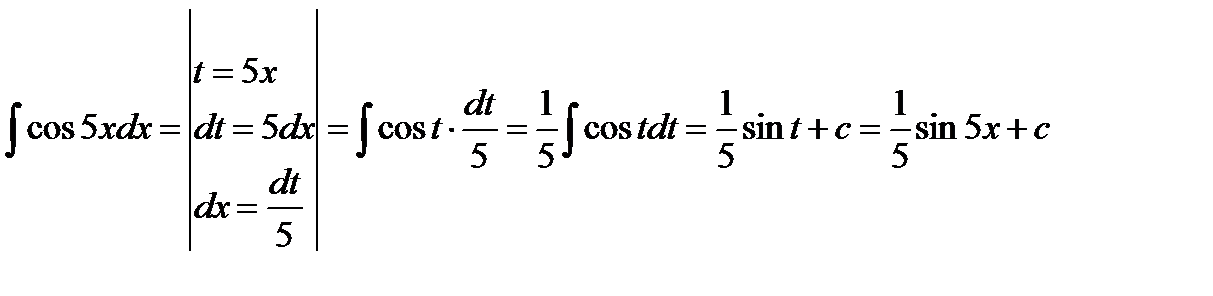

Обратим внимание на то, что под знаком косинуса стояло выражение 5 х и в ответе мы получи коэффициент только в виде обратной дроби . Заметим, что данный интеграл является табличным.

Аналогично решаются остальные два интеграла, также являющиеся табличными.

б)

в) .