Пусть u = u (x)и v = v (x) – дифференцируемые функции, тогда справедлива формула
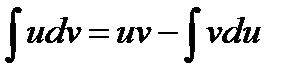 . (*)
. (*)
Формула (*) называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подынтегрального выражения на два сомножителя (u и dv). При переходе к правой части формулы (*) первый из них дифференцируется (при нахождении дифференциала: 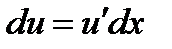 ), второй интегрируется (
), второй интегрируется (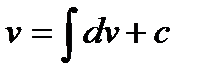 ).
).
Возможность применения формулы (*) связана с тем, дифференцирование может существенно упростить один из сомножителей (при условии, что интегрирование не слишком усложнит другой.)
Рассмотрим интегралы Iтипа
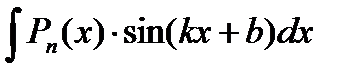 ;
;  ;
; 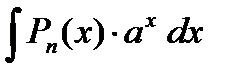
В данных интегралах выбирают u = Pn (x), а за dv – оставшийся множитель.
Пример 9. Найти 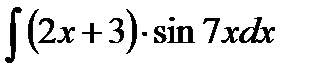
Выполняем замену u =2 x +3 и dv =sin7 xdx, необходимо найти du и v.
du = d (2 x +3)=2 dx,
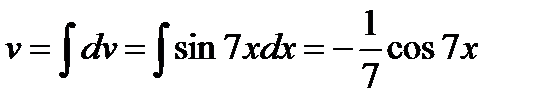 тогда, получим
тогда, получим
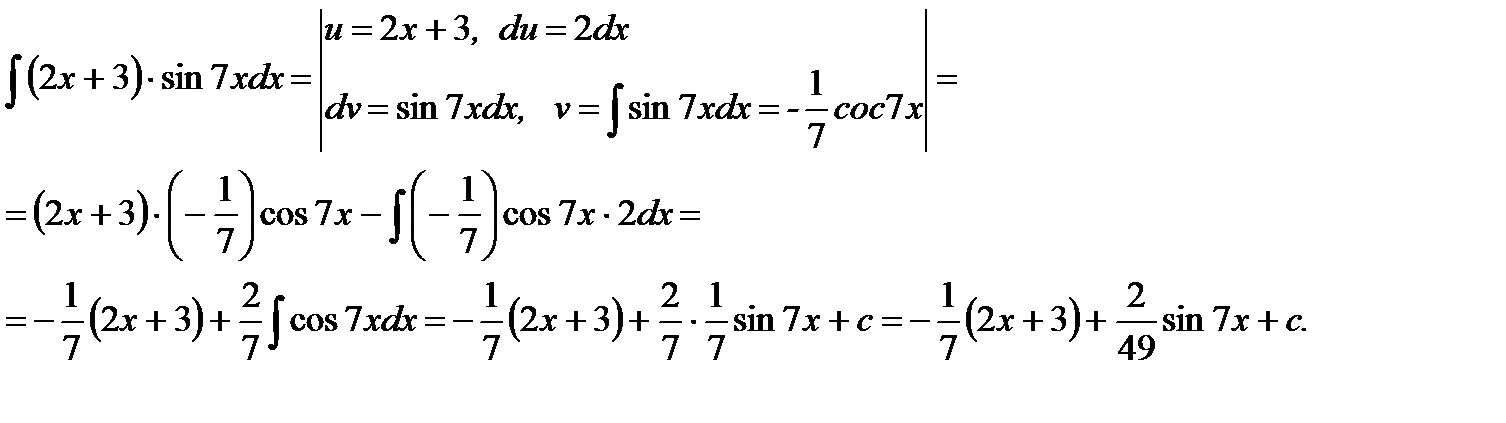
Рассмотрим интегралы II типа.
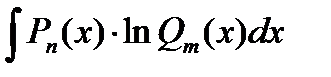 ;
; 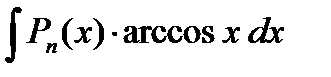 ;
; 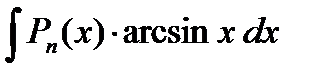 ;
;
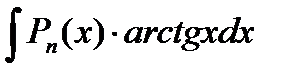 ;
; 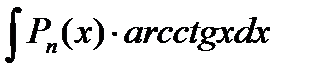
В данных интегралах выполняют замену dv = Pn (x), а за u = оставшийся множитель.
Пример 10. Найти 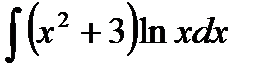
В данном интеграле делаем замену u = ln x и dv = x 2+3, найдем du и v.
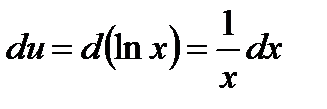 . См. таблицу производных.
. См. таблицу производных.
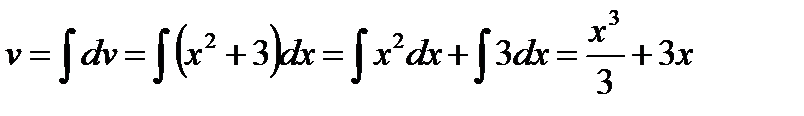 , тогда
, тогда
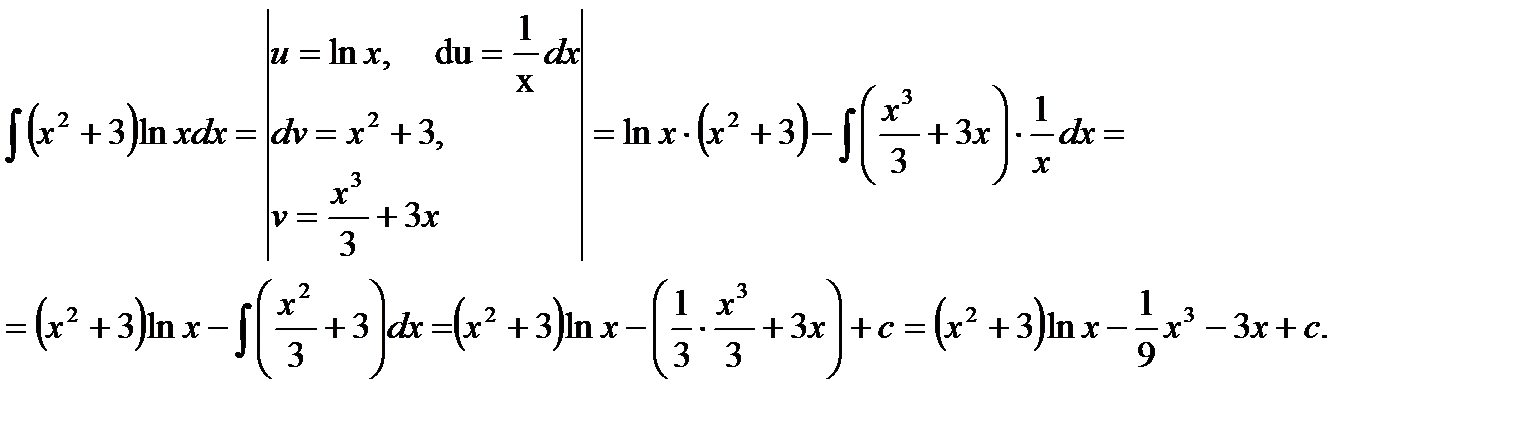
Замечание. При решении интегралов возможно применение формулы интегрирования по частям два и более раз, в тех случая, когда в интегралах I типа многочлен Pn (x) второй и выше степени.
Пример11. Найти 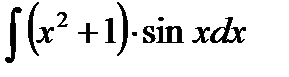
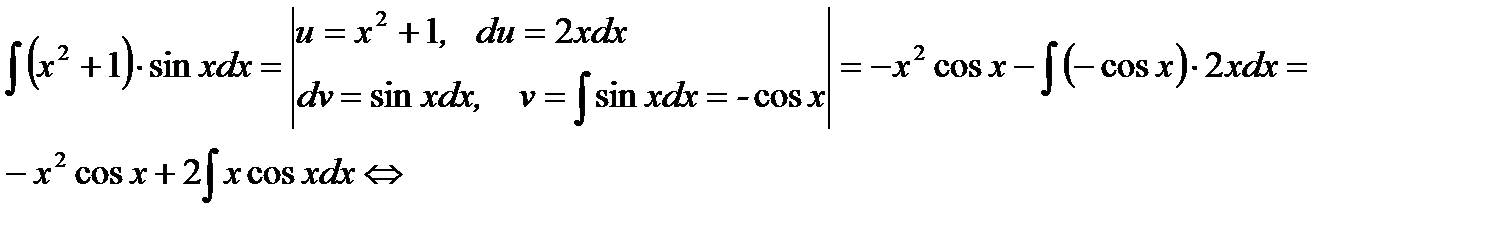
Возникший интеграл 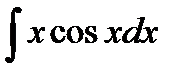 не является табличным, однако, видно, что по сравнению с исходным интегралом степень переменной х в подынтегральном выражении уменьшилась на единицу, при этом второй сомножитель cosx того же типа, что в исходном интеграле. Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Применим формулу интегрирования по частям к интегралу
не является табличным, однако, видно, что по сравнению с исходным интегралом степень переменной х в подынтегральном выражении уменьшилась на единицу, при этом второй сомножитель cosx того же типа, что в исходном интеграле. Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Применим формулу интегрирования по частям к интегралу 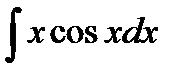 .
.
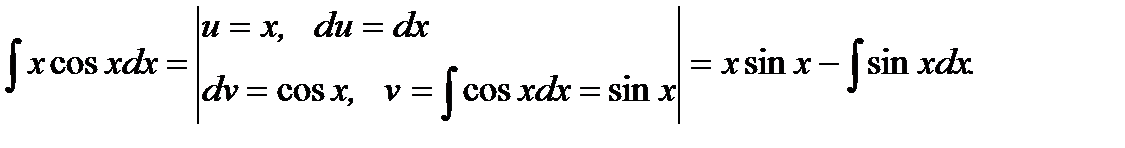
Подставим получившийся результат в решение данного интеграла, и получим
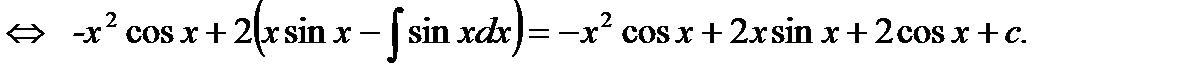
 2017-12-14
2017-12-14 1790
1790
