Вычисление площади фигуры

Пусть функция y = f (x) неотрицательна и непрерывна на отрезке [ a, b ]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой y = f (x) на [ a, b ] численно равна определенному интегралу , т.е.

Пример: Найти площадь фигуры, ограниченной линиями

Решение:

Искомая площадь S криволинейного треугольника OAB равна разности двух площадей:

S = S_OABC – S_OBC,

каждая из которых находится по геометрическому смыслу определенного интеграла.

Решая систему ,получаем что точка В пересечения прямой y =4и кривой имеет координаты (2; 4).

Тогда

.

Задания для самоконтроля

 

1. Вычислите неопределенный интегралы:

 

а)	д)
б)	е)
в)	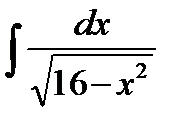ж)
г)	з)

 

2. Вычислите определенные интегралы:

а)	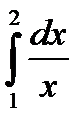д)
б)	е)
в)	ж)
г)	з)

 

3. Вычислить площадь фигуры, ограниченной линиями:

а) , , , .

б) , , , .

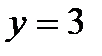в) .

г) .

РАЗДЕЛ 4. ЧИСЛЕННЫЕ МЕТОДЫ

 

Численное дифференцирование