Особенность задачи численного дифференцирования

Когда производную аналитически заданной функции по причине ее сложности искать затруднительно, либо выражение для производной приобретает слишком неудобную для применений форму, используют приближенное, или численное, дифференцирование. Этот метод тем более необходим, если исходная функция задана таблично. Один из способов решения задачи дифференцирования – использование интерполяционных многочленов.

Пусть f (x) – функция, для которой нужно найти производную в заданной точке отрезка [ a, b ], а F_n (x)– интерполяционный многочлен для f (x), построенный на отрезке [ a, b ]. Заменяя f (x) интерполяционным многочленом F_n (x), получим значение производной f (x) на отрезке[ a, b ]как значение производной 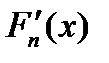интерполяционного многочлена, т.е. примем приближенно

(1)

Аналогичным путём можно поступать при нахождении значений производных высших порядков функции f (x). Полагая, что погрешность интерполирования определяется формулой

R_n (x)= f (x) – F_n (x)

получаем подход к оценке погрешности производной :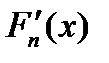

(2)

т.е. погрешность производной интерполируемой функции равна производной от погрешности этой функции.

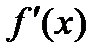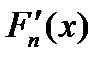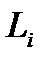Заметим, однако, что задача численного дифференцирования является некорректной. Дело в том, что погрешность производной интерполяционного многочлена может существенно превышать погрешность самой интерполяции. Из рисунка 1 хорошо видно, что даже незначительное отличие (в том числе и совпадение) значений f (x) и F_n (x) никак не гарантирует близости значений их производных и ( и 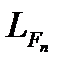– касательные к кривым f (x) и F_n (x) соответственно). Рассмотрим методы численного дифференцирования на основе интерполяционных многочленов Лагранжа и Ньютона