Интерполяционная формула Лагранжа для равноотстающих узлов

Применяя для численного дифференцирования на отрезке[ a, b ]интерполяционный полином, естественно строить на этом отрезке систему равноотстоящих узлов , которыми отрезок делится на n равных частей: (i = 0,1, 2,..., n − 1). В этом случае шаг интерполирования имеет значение

h = (b − a)/ n,

а интерполяционный многочлен Лагранжа (как и интерполяционные многочлены Ньютона) строится на равноотстоящих узлах и имеет более удобный вид. Примем подстановку:

(3)

с учётом представления:

получим новые выражения для 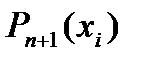. Учитывая, что согласно принятому обозначению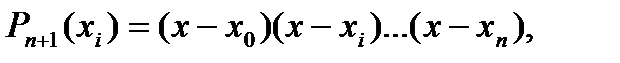

и используя (3), последовательно находим:

т.е. вобщемслучае:

(i = 0,1, 2,..., n)(4)

Используя (4), получаем:

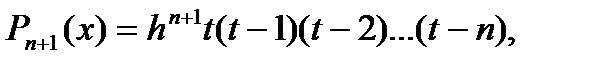
Сцельюсокращениязаписейвведёмобозначение

тогдавыражение принимаетвид:

(5)

Учитывая, чтоприпостоянномшагеимеетместо

(i = 0,1, 2,..., n)

последовательнонаходим:

(6)

…………………………

.

Заметим, чтов (6) ровно n строк (i -ястрокаотсутствует), причёмзначенияразностейизпервых i строкположительны, аостальных – отрицательны. Используя (6), получаем:

т.е.

(7)

С учётом представлений (5) и (7) формула Лагранжа (лекция №5, (9)) для равноотстоящих узлов принимает вид:

(8)

Пример 1. Составить интерполяционный многочлен Лагранжа для функции, заданной своими значениями на равноотстоящих узлах (n =2, h = 1):

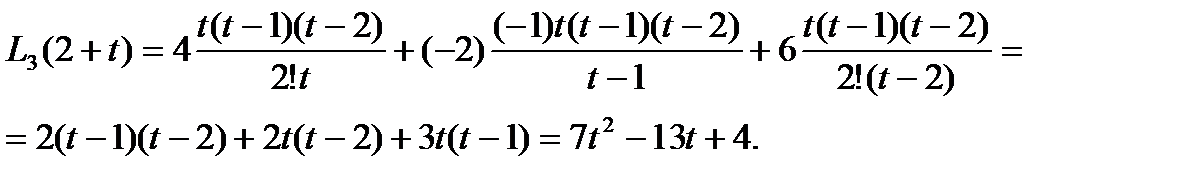
Узловые табличные значения функции (4; -2; 6) получаются по этой формуле соответственно при t = 0; 1; 2.