Рассмотрим 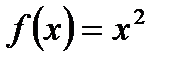 и найдем значение функции в точке π:
и найдем значение функции в точке π: 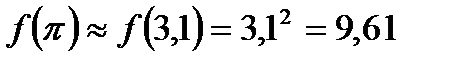 . Точнее
. Точнее  .
.
2) Аналогично для 
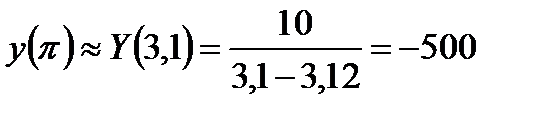
 (!)
(!)
Мы видим, что для функции f ее значения в точках х=3,1 и х=3,14 мало отличаются между собой, а для другой функции У сильно отличаются. Эффект объясняется тем, что в первом случае имеем дело с непрерывной функцией, а во втором – с разрывной (см. рис.
3, 4).
Следовательно, вычисления с разрывными функциями надо проводить осторожно. А для этого их надо уметь отличать до построения графика.
Перед нами стоит задача сформулировать определение непрерывности функции в точке х=а. Хотя интуитивно понятие непрерывной функции ассоциируется с «непрерывностью» ее графика, но мы не можем это условие принять за определение непрерывности функции. Определение должно носить аналитический характер. Действительно, во-первых, анализ не может опираться на геометрию. Наоборот, в самой геометрии непрерывность линии определяется с помощью понятия непрерывной функции. Во-вторых, в самом анализе аналитическое исследование должно предшествовать построению графика. В-третьих, непрерывность функций обычно устанавливается не по самому определению, а на основании рассматриваемых нами позже теорем, которые доказываются с использованием именно аналитического определения непрерывности. Геометрически их доказать невозможно. Обозначим 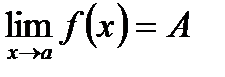 , где
, где 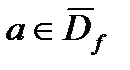 .Возможны следующие 4 случая:
.Возможны следующие 4 случая:
1) А - существует,  - не существует (рис. 5).
- не существует (рис. 5).
2) А - не существует
3) А – не существует
 - существует (рис. 6)
- существует (рис. 6)  -не существует (рис. 7)
-не существует (рис. 7)
4) А – существует,  - существует (рис. 8).
- существует (рис. 8).
В 4-ом случае верна теорема:
Теорема: Если в данной точке функция имеет как значение, так и предел, то они равны между собой, т.е.

Проведенная классификация показывает, что непрерывность графика получается только в последнем случае. Его и примем за определение:
Определение: Функция f называется непрерывной в точке а, если в этой точке существуют как ее значения, так и предел. При этом мы доказали, что предел и значение равны между собой, если они оба существуют.
Это определение можно перефразировать по Гейне и по Коши:
Определение Гейне: Функция f называется непрерывной в точке а, если 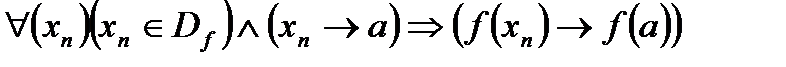 .
.
Определение Коши: Функция f называется непрерывной в точке а, если 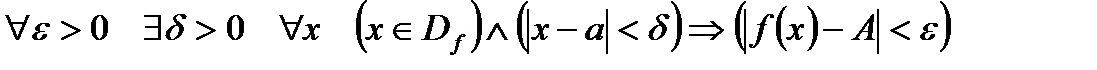 .
.
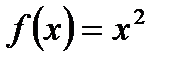 и найдем значение функции в точке π:
и найдем значение функции в точке π: 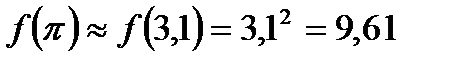 . Точнее
. Точнее  .
.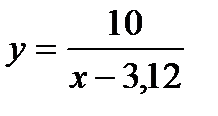

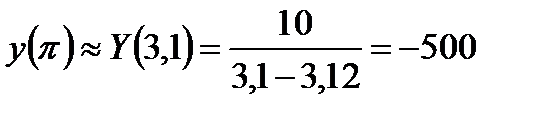
 (!)
(!)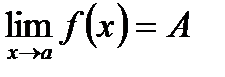 , где
, где 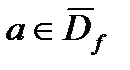 .Возможны следующие 4 случая:
.Возможны следующие 4 случая: - не существует (рис. 5).
- не существует (рис. 5). - существует (рис. 6)
- существует (рис. 6)  -не существует (рис. 7)
-не существует (рис. 7) - существует (рис. 8).
- существует (рис. 8).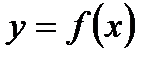

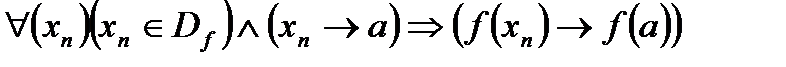 .
.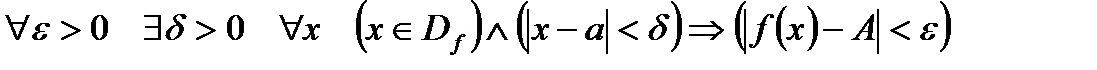 .
. 2017-12-14
2017-12-14 718
718








