Пусть даны множества X, Y, Z и функции  , (т.е.
, (т.е.  ) и
) и 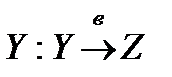 . Тогда композиция этих функций дает новую функцию:
. Тогда композиция этих функций дает новую функцию: 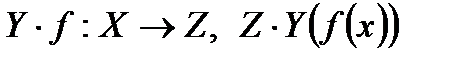 - сложная функция.
- сложная функция.
Например,
1)  где
где  , т.е.
, т.е. 
2)  где
где  , т.е.
, т.е. 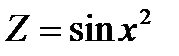
3) 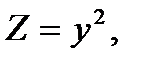 где
где  , т.е.
, т.е. 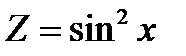
В последнем случает, например,  , а
, а 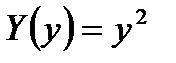 , т.е. сложная функция имеет вид:
, т.е. сложная функция имеет вид:  .
.
Теорема о пределе сложной функции: Если существует
1) 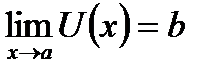 2)
2) 
Тогда существует  , и
, и  .
.
Примеры 1) 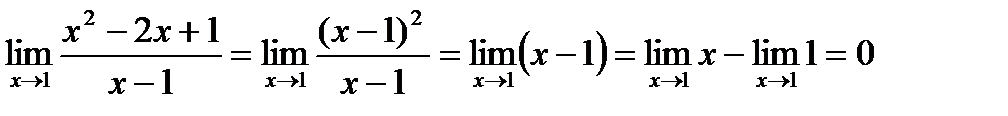
В этом решении возникает вопрос о возможности сокращения дроби при переходе к пределу. Эта возможность объясняется так. Функция  не определена в точке 1. Поэтому ее предел зависит только от ее поведения в проколотой окрестности 1, а в проколотой окрестности эта функция полностью совпадает с функцией х-1. Поэтому пределы этих функций равны.
не определена в точке 1. Поэтому ее предел зависит только от ее поведения в проколотой окрестности 1, а в проколотой окрестности эта функция полностью совпадает с функцией х-1. Поэтому пределы этих функций равны.
2) 

В предпоследнем равенстве использована теорема о пределе сложной функции и свойство, что  .
.
3) 
В последнем равенстве использована теорема о пределе сложной функции. Здесь  .
.
Предел функции на бесконечности.
Если 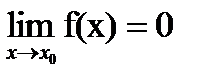 , то функция f(х) называется бесконечно малой в окрестности точки х0.
, то функция f(х) называется бесконечно малой в окрестности точки х0.
Например: функция у=х-4 при х  4 является бесконечно малой.
4 является бесконечно малой.
|
|
|
Если  или
или  , то функция называется бесконечно большой в окрестности точки х0.
, то функция называется бесконечно большой в окрестности точки х0.
Например: у=х3 при x  является бесконечно большой
является бесконечно большой
Замечание: д анные выше определения справедливы и при x  ±
±  .
.
Непрерывные функции, их свойства. Односторонние пределы. Точки разрыва и их классификация.
 2017-12-14
2017-12-14 1731
1731
