Односторонние пределы, признак существования предела функции в точке. Точки разрыва и их классификация

Определение: Функция называется непрерывной на некотором множестве, если она непрерывна в каждой точке этого множества.

1) . Эта функция непрерывна в любой точке на R (см. 17, пример 4).

2) 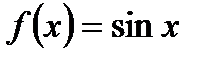непрерывна на R. Для доказательства достаточно показать, что для будет . Воспользуемся определением Коши. Возьмем . Тогда

Достаточно взять . Тогда

Аналогично можно доказать непрерывность косинуса.

Введем термины и обозначения.

Левый предел функции: .

Правый предел: .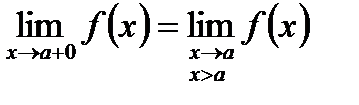

Теорема: Если в (.) х₀ существуют односторонние пределы, они равны между собой и равны А, то в точке х₀ существует предел функции, и он равен А.