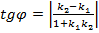Метрическая теория прямых на плоскости

– тангенс острого угла между двумя прямым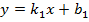и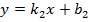

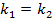и ;

и 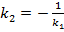– условия параллельности и перпендикулярности двух прямых 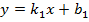и ;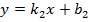

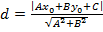– расстояние от точки 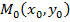до прямой Ах + By + С = 0;

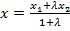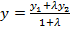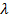, , ≠ –1 - координаты точки М(х, у), делящей отрезок 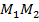в отношении , , ;

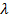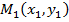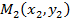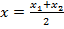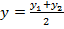, – координаты середины отрезка , , .

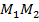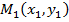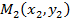14) 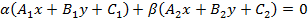– уравнение пучка прямых, проходящих через точку пересечения прямых 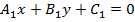и .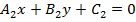

Пусть на плоскости заданы точкаМ₀(х ₀; у₀)и прямаяАх + Ву+ С = 0. Под расстояни­ем от точки М₀ до прямойАх + Ву+ С = 0при­нимается длина перпендикуляра, опущенного из точки М₀на прямую. Данное расстояние можно определить по формуле: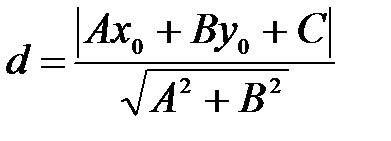

1.2Лекция 2 (2 ч.)

Тема: Теория пределов и непрерывность функции в точке. Производная функции в точке, ее геометрический смысл.

1.2.1 Вопросы лекции:

1. Понятие предела функции в точке. Свойства функций, имеющих предел в точке, арифметические действия над пределами.

2. Непрерывность функции в точке.

3. Производная функции в точке, правила дифференцирования

1.2.2. Краткое содержание вопросов: