2017-12-14
510
Метод интегрирования с помощью этой таблицы и свойств неопределенных интегралов обычно называют методом непосредственного интегрирования.
Примеры:
1. 
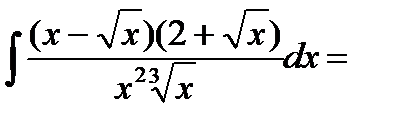(перемножаем скобки в числителе)=
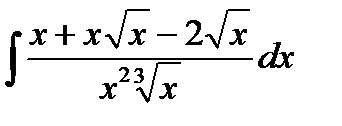= (записываем «корни» в виде степеней с дробными показателями)= 
(делим почленно числитель на знаменатель)=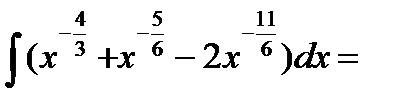 
(применяем свойство 4 и формулу 2 из ТОИ)=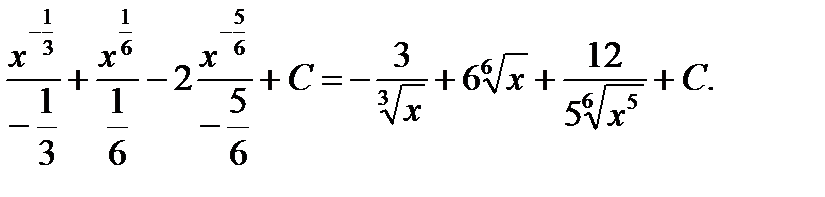 
2. 
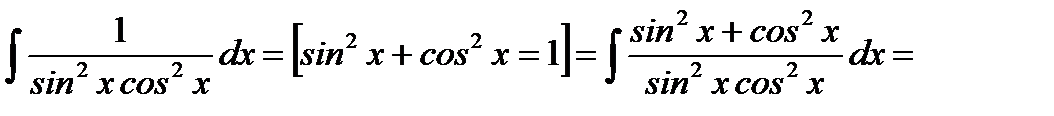(делим почленно числитель на знаменатель) = 
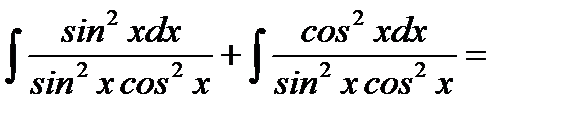(применяем формулы 7,8 ТОИ)= tgx-ctgx+C
3. 
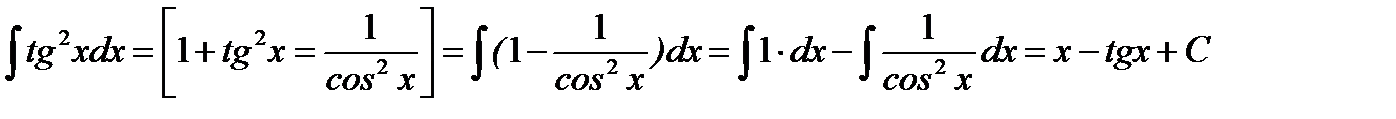
4. 
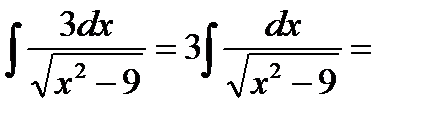(по формуле 12 ТОИ)= 3ln|x+ 
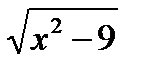|+C.
Одним из самых сильных методов интегрирования является метод подстановки. В его основе лежит легко проверяемая формула:
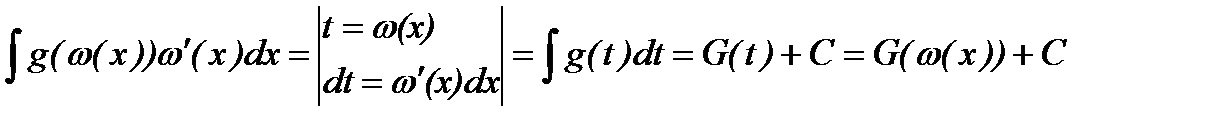
Эту формулу следует применять тогда, когда первообразная для g(t) известна или легко находится.
Примеры:
1. 
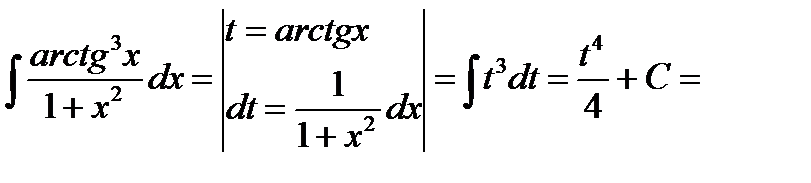(делаем обратную подстановку) =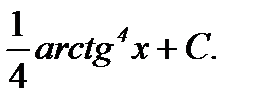 
2. 
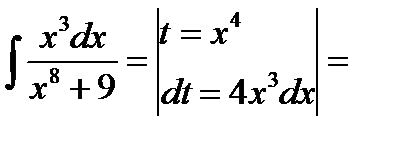(умножаем числитель и знаменатель на 4)= = 
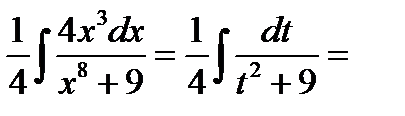(формула 13 ТОИ)=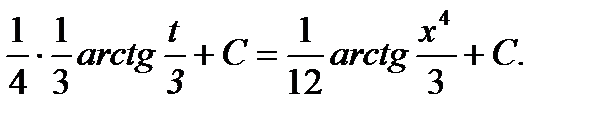 
В некоторых случаях полезны специальные подстановки.
3. 
=
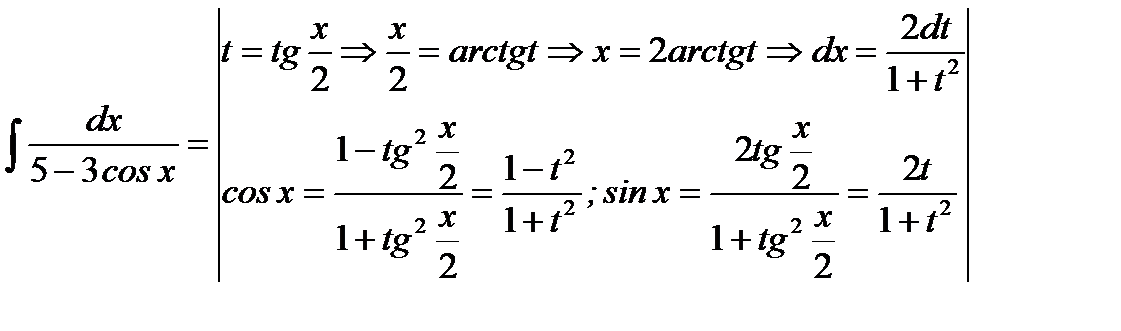(это «универсальная» подстановка, которая применяется при интегрировании рациональных выражений от тригонометрических функций)=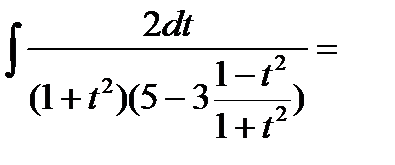 
(выполняем тождественные преобразования)= 
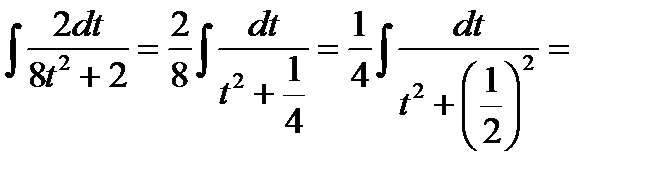(формула 12 ТОИ)
= 
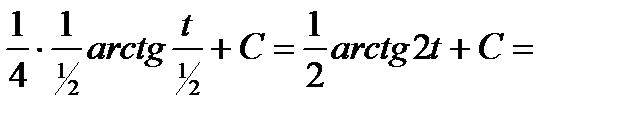(переходим к «х») = 
.
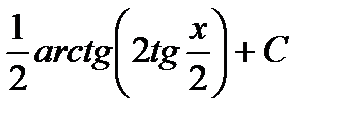4. J =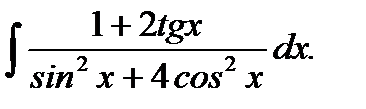 
При нахождении этого интеграла можно применить «универсальную» подстановку, но можно обойтись и без нее, сделав следующие преобразования:
1) в знаменателе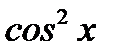 
вынесем за скобки, получим: J =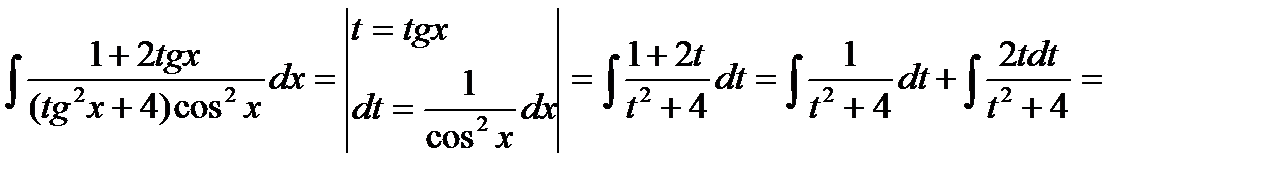 
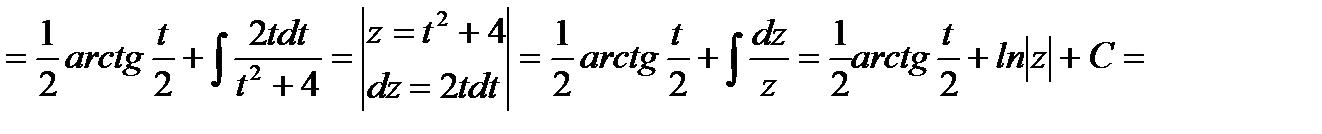
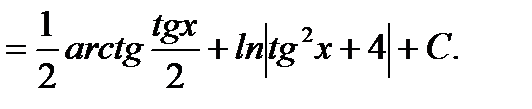
5. J =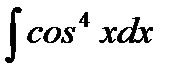 
.
При четном показателе степени обычно применяют формулу «понижения степени» за счет перехода к двойному аргументу:
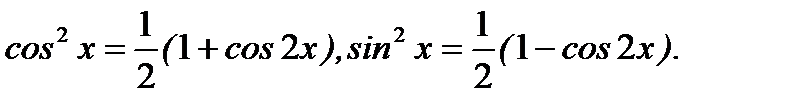В нашем случае будем иметь: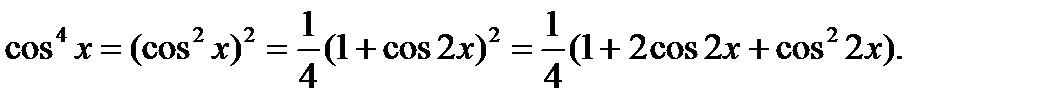 
Поэтому
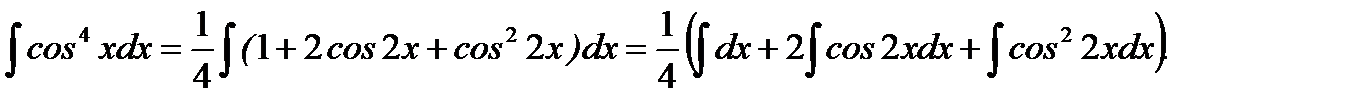Второй интеграл в скобках преобразуется к виду:
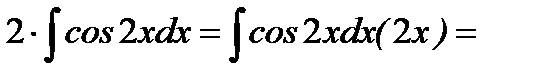(формула 5 ТОИ)= sin2x+C.
Для вычисления третьего интеграла еще раз применим формулу «понижения степени»:
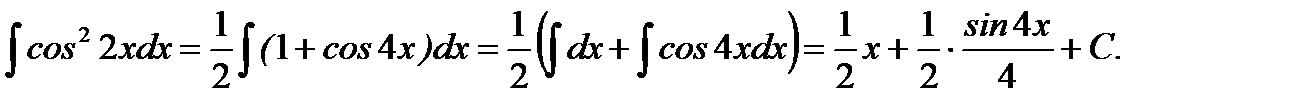
Окончательно будем иметь:
J = 
6. 
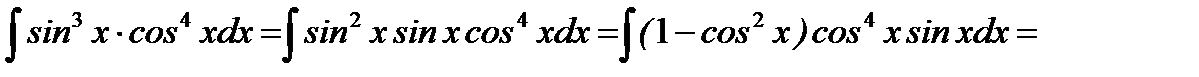
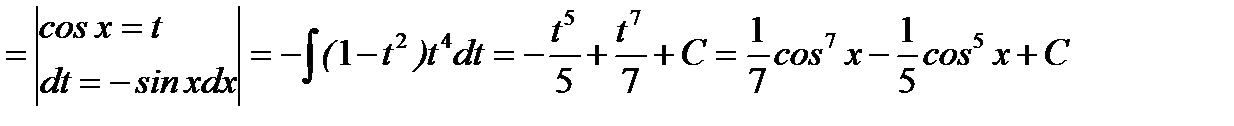
Метод интегрирования по частям основан на применении следующей формулы: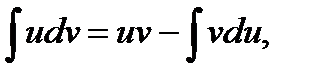 
где u(x),v(x) - непрерывные и дифференцируемые на промежутке Х функции.
Эта формула обычно бывает полезна при интегрировании функций следующего вида:
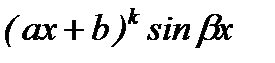(u=(ax+b)k)
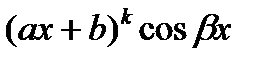(u=(ax+b)k)
(u=lnx)
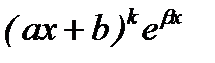(u=(ax+b)k)
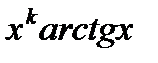(u=arctgx)
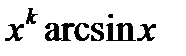(u=arcsinx)
Примеры:
1. 
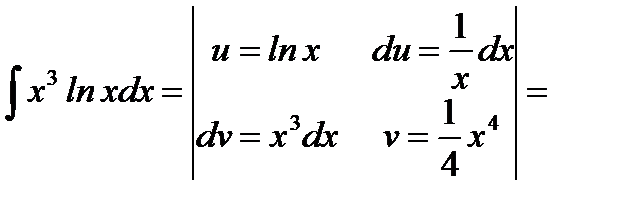(подставляем в правую часть формулы)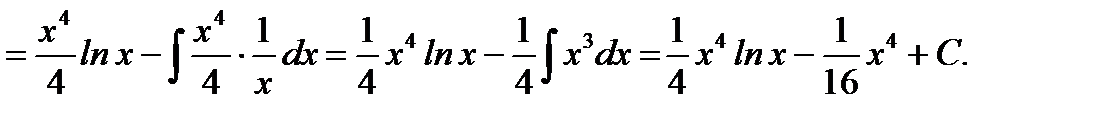 
3. Определенный интеграл, методы вычисления.
