Первообразная и неопределенный интеграл, свойства

Основная задача дифференциального исчисления состоит в нахождении дифференциала данной функции или ее производной. Интегральное исчисление решает обратную задачу:по заданному дифференциалу, а, следовательно, и производной неизвестной функции F(x), требуется определить эту функцию. Иными словами, имея выражение

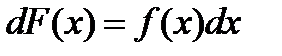(1)

или соответственно

,

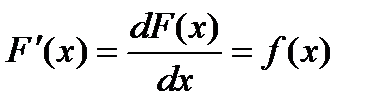где f(x) – известная функция, нужно найти функцию F(x). Искомая функция F(x) называется при этом первообразной функцией по отношению к функции f(x). Для простоты мы будем предполагать, что равенство (1) выполняется на некотором конечном или бесконечном промежутке.

Определение: Первообразной функциейдля данной функции f(x) на данном промежутке называется такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке.

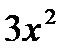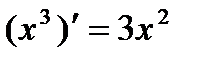Например, одной из первообразных функций для функции будет , ибо . Первообразная функция не единственна, так как 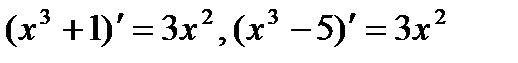и т.д., и поэтому функции и т.п. также являются первообразными для функции 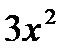. Следовательно, данная функция имеет бесчисленное множество первообразных.

В нашем примере каждые две первообразные отличались друг от друга на некоторое постоянное слагаемое. Покажем, что это будет иметь место и в общем случае.

Теорема: Две различные первообразные одной и той же функции, определенной на некотором промежутке, отличаются друг от друга на этом промежутке на постоянное слагаемое.

Доказательство: В самом деле, пусть f(x) – некоторая функция, определенная на промежутке 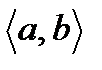, и F₁(x), F₂(x) – ее первообразные, т.е.

и .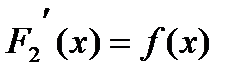

Отсюда .

y=F1(x)

y=F2(x)

F1(x)

F2(x)

С

М2

М1

х

α

X

α

Y

Рис. 1.

Но если две функции имеют одинаковые производные, то эти функции отличаются друг от друга на постоянное слагаемое. Следовательно,

F₁(x) - F₂(x) = С,

где С – постоянная величина. Теорема доказана.

Рассмотрим геометрическую иллюстрацию. Если у = F₁(x) и Y = F₂(x)

- первообразные одной и той же функции f(x), то касательные к их графикам в точках с общей абсциссой х параллельны между собой (рис. 1):

tgα = = f(x).

В таком случае расстояние между этими кривыми вдоль оси Оу остается постоянным: F₂(x) – F₁(x) = С, т.е. эти кривые в некотором смысле «параллельны» друг другу.

Следствие: Прибавляя к какой-либо первообразной функции f(x), определенной на промежутке 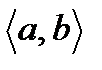, все возможные постоянные С, мы получим все первообразные для функции f(x).

В самом деле, если F(x) есть первообразная функция для f(x), то функция F(x)+C, где С - любая постоянная, также будет первообразной функции f(x), так как .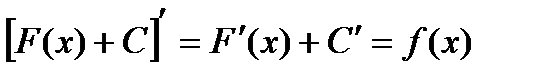

С другой стороны, мы доказали, что каждая первообразная функции f(x) может быть получена из функции F(x) путем прибавления к ней надлежащим образом подобранного постоянного слагаемого С.

Следовательно, выражение F(x) + С, где 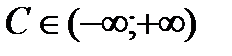, (2)

где F(x) – какая-либо первообразная для функции f(x), исчерпывает всю совокупность первообразных для данной функции f(x).

В дальнейшем мы будем предполагать, если явно не оговорено противное, что рассматриваемая функция f(x) определена и непрерывна на некотором конечном или бесконечном промежутке .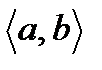

Введем теперь основное понятие интегрального исчисления – понятие неопределенного интеграла.

Определение: Общее выражение для всех первообразных данной непрерывной функции f(x) называется неопределенным интегралом от функции f(x) или от дифференциального выражения f(x)dx и обозначается символом .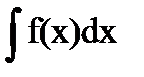

При этом функция f(x) называется подынтегральной функцией, а выражение f(x)dx называется подынтегральным выражением.

Согласно определению неопределенного интеграла можно записать

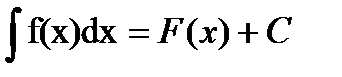, (3)

С4

С3

С2

С1

X

Y

Рис. 2.

где , постоянная С может принимать любое значение, и поэтому называется произвольной постоянной.

Пример. Как мы видели, для функции 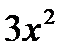одной из первообразных является функция 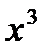. Поэтому .

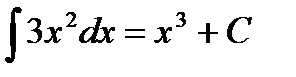Геометрически неопределенный интеграл у=F(x)+C представляет собой семейство «параллельных» кривых (рис.2).