Пусть дан определенный интеграл 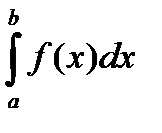 , где f(x) – непрерывная на отрезке [ a,b ] функция. Допустим, по каким-то соображениям нам желательно ввести новую переменную t, связанную с прежней переменной х соотношением: х=φ (t) (α≤t≤ β), где φ (t) – непрерывно дифференцируемая на отрезке [ a,b ] функция. Если при этом: 1) при изменении t от α до β переменная х меняется от a до b, т.е. φ(α)=а, φ(β) =b; 2) сложная функция f(φ(t)) определена и непрерывна на отрезке [ α,β ], то справедлива формула
, где f(x) – непрерывная на отрезке [ a,b ] функция. Допустим, по каким-то соображениям нам желательно ввести новую переменную t, связанную с прежней переменной х соотношением: х=φ (t) (α≤t≤ β), где φ (t) – непрерывно дифференцируемая на отрезке [ a,b ] функция. Если при этом: 1) при изменении t от α до β переменная х меняется от a до b, т.е. φ(α)=а, φ(β) =b; 2) сложная функция f(φ(t)) определена и непрерывна на отрезке [ α,β ], то справедлива формула 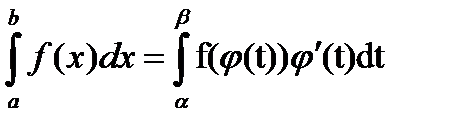 .
.
Замечание: При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к прежней переменной, достаточно лишь ввести новые пределы интегрирования.
Пример. Вычислить 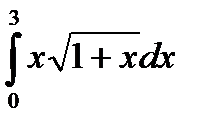 .
.
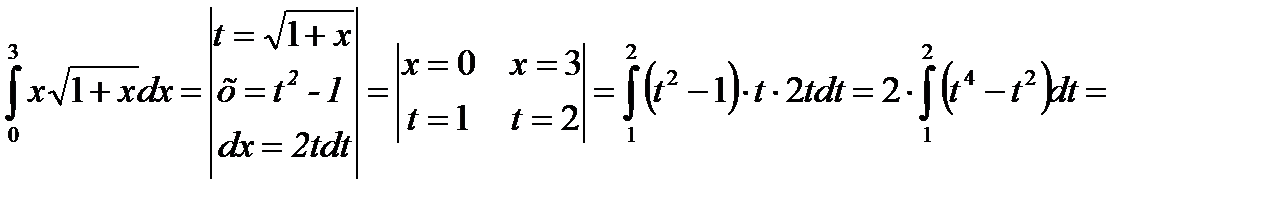
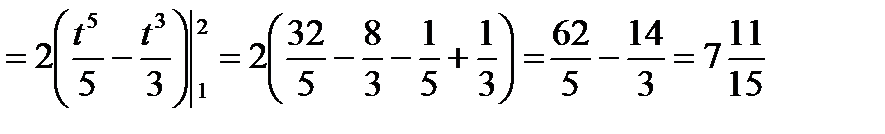 .
.
4. Применение определенного интеграла к вычислению площади плоской фигуры.
Формулы для нахождения площади плоской фигуры:
в декартовой системе координат (рис.1) 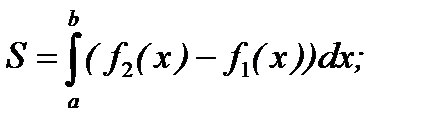 (1)
(1)
в полярной системе координат (рис.2)
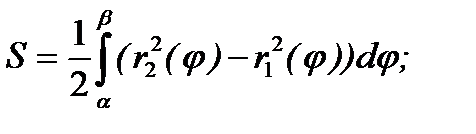
(2)
в случае параметрического задания кривой
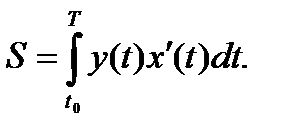
(3)
1. Найти площадь области, ограниченной графиками функций 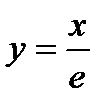 и y=xe-x.
и y=xe-x.
Решение. Строим графики функций 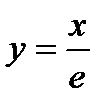 и y=xe-x в одной системе
и y=xe-x в одной системе
координат. При этом график функции y=xe-x строим, предварительно проведя ее полное исследование.
Находим точки пересечения кривых
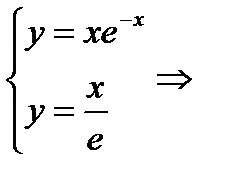
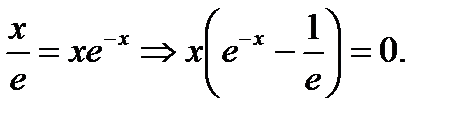 Отсюда
Отсюда 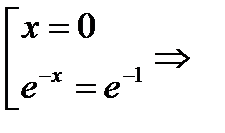
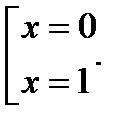
Площадь области находим по формуле (18): 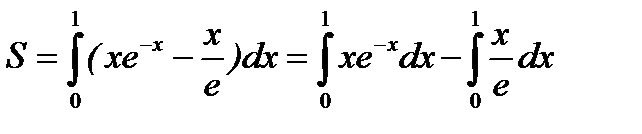
Первый интеграл берется методом интегрирования по частям, второй интеграл табличный (предлагаем выполнить интегрирование самостоятельно). Окончательно 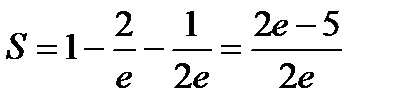 (кв. ед.).
(кв. ед.).
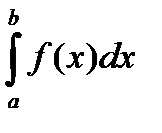 , где f(x) – непрерывная на отрезке [ a,b ] функция. Допустим, по каким-то соображениям нам желательно ввести новую переменную t, связанную с прежней переменной х соотношением: х=φ (t) (α≤t≤ β), где φ (t) – непрерывно дифференцируемая на отрезке [ a,b ] функция. Если при этом: 1) при изменении t от α до β переменная х меняется от a до b, т.е. φ(α)=а, φ(β) =b; 2) сложная функция f(φ(t)) определена и непрерывна на отрезке [ α,β ], то справедлива формула
, где f(x) – непрерывная на отрезке [ a,b ] функция. Допустим, по каким-то соображениям нам желательно ввести новую переменную t, связанную с прежней переменной х соотношением: х=φ (t) (α≤t≤ β), где φ (t) – непрерывно дифференцируемая на отрезке [ a,b ] функция. Если при этом: 1) при изменении t от α до β переменная х меняется от a до b, т.е. φ(α)=а, φ(β) =b; 2) сложная функция f(φ(t)) определена и непрерывна на отрезке [ α,β ], то справедлива формула 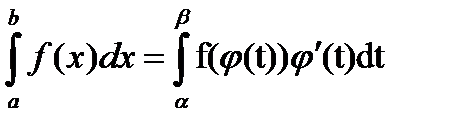 .
.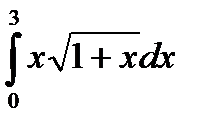 .
.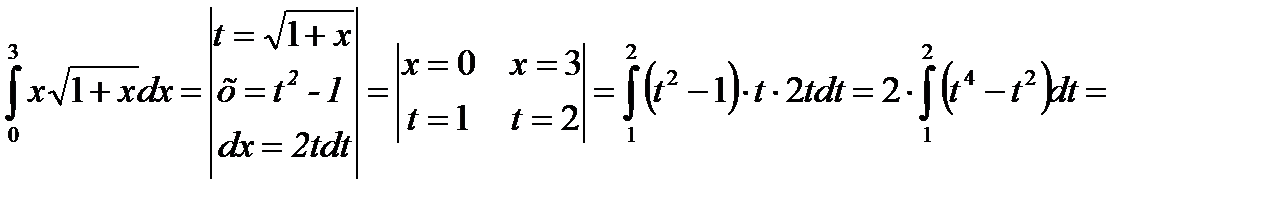
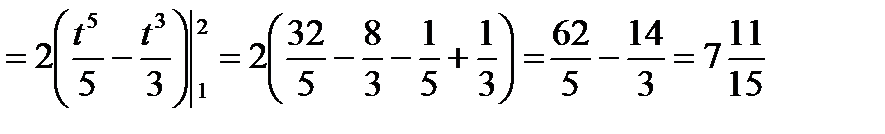 .
.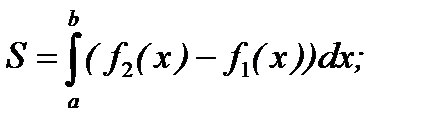 (1)
(1)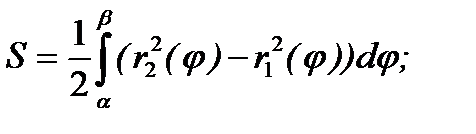 (2)
(2)
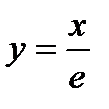
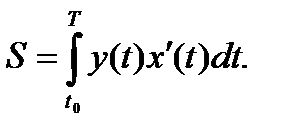 (3)
(3)
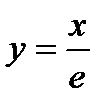 и y=xe-x.
и y=xe-x.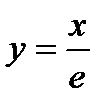 и y=xe-x в одной системе
и y=xe-x в одной системе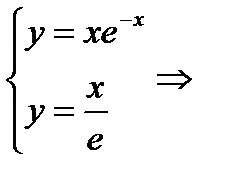
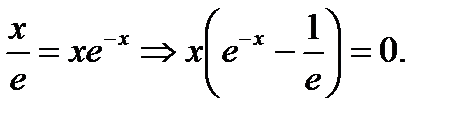 Отсюда
Отсюда 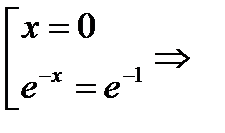
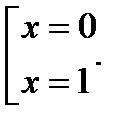
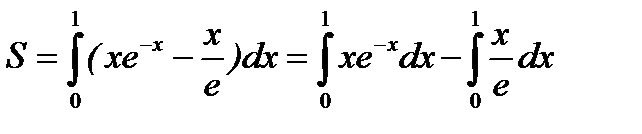
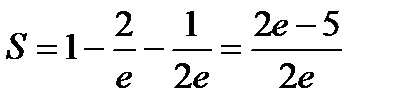 (кв. ед.).
(кв. ед.). 2017-12-14
2017-12-14 577
577








