Пусть u=u(x), υ=υ(х) – непрерывно дифференцируемые на отрезке [ a,b ] функции. Имеем: 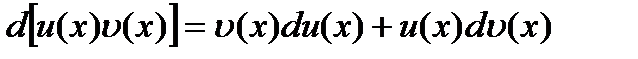 .
.
Интегрируя это равенство в пределах от a до b и учитывая, что
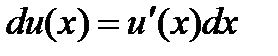 и,
и, 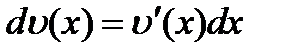 ,
,
Находим
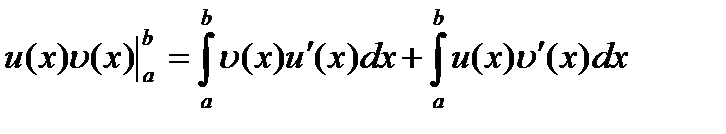 .
.
Отсюда получаем формулу интегрирования по частям в определенном интеграле
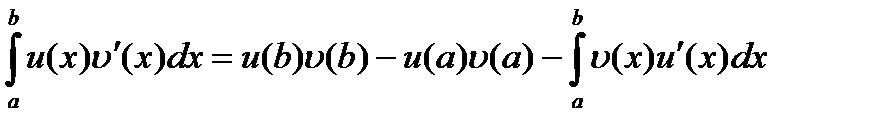 . (17)
. (17)
Для краткости употребляется обозначение
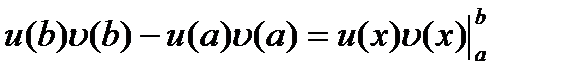 .
.
Пример. Найти 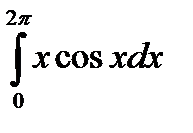 .
.
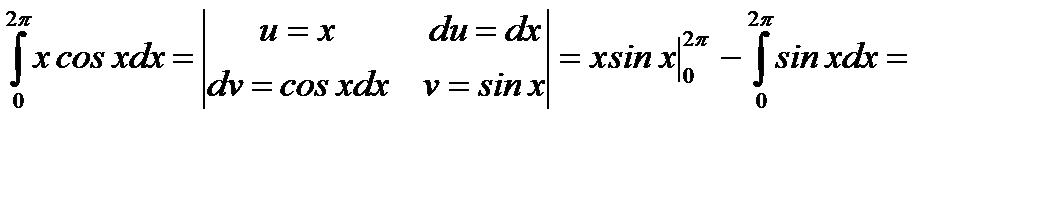 .
.
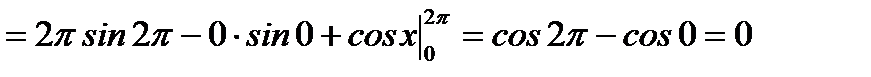
 2017-12-14
2017-12-14 418
418








