Логарифмическое нормальное распределение. При логарифмическом нормальном распределении логарифм случайной величины распределяется по нормальному закону

 

При логарифмическом нормальном распределении логарифм случайной величины распределяется по нормальному закону. Это распределение несколько точнее нормального распределения описывает наработку деталей, т.к. представляет собой распределение положительных величин. Этот закон успешно применяют, например, для описания наработки подшипников качения.

Логарифмическое нормальное распределение удобно для случайных величин, представляющих собой произведение значительного числа случайных исходных величин, подобно тому, как нормальное распределение удобно для суммы случайных величин. Логарифмическое нормальное распределение – распределение двухпараметрическое с плотностью распределения (рис. 1.9)

,

где и - параметры распределения.

 

Рисунок 1.9 – Логарифмическое нормальное распределение:

а – вероятность безотказной работы, б – плотность вероятности отказа,

в – интенсивность отказов.

Вероятность безотказной работы

Интенсивность отказов .

Функции и определяются по таблицам для нормального распределения в зависимости от квантиля .

Для логарифмического нормального распределения характерно возрастание интенсивности отказов с увеличением срока эксплуатации. Оно имеет следующие числовые характеристики.

Средняя наработка .

Дисперсия .

Коэффициент вариации .

Математическое ожидание наработок до отказа .

Среднее квадратичное отклонение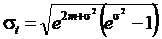

Здесь , .

Следует отметить, что для вероятности безотказной работы и коэффициента вариации логарифмический нормальный закон можно заменить нормальным законом с параметрами и 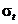и плотностью

.

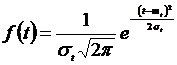Пример 1.10. Наработка до отказа подшипника скольжения привода конусной дробилки имеет логарифмически нормальное распределение с параметрами m = 4 и s = 1. Найти вероятность безотказной работы и интенсивность отказов при наработке t = 60 суток и определить величину средней наработки.

Решение.

Вероятность безотказной работы равна

Здесь Ф(0,04) = 0,036 – табличное значение (Приложение Г).

Интенсивность отказов

.

Здесь φ(0,04) = 0,3973 – табличное значение (Приложение Б).

Средняя наработка равна

суток.