2017-12-14
8628
Экспоненциальным законом называют распределение, для которого вероятность безотказной работы описывается показательным законом (рис. 1.4)
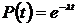. (1.1)
Так как интенсивность отказов не зависит от возраста изделия (отказы в период нормальной работы), то
. (1.2)
Соответственно, плотность вероятности отказов будет
. (1.3)
Числовые характеристики экспоненциального закона распределения
- интенсивность отказов 
;
- средняя наработка до отказа 
;
- дисперсия 
;
- среднее квадратичное отклонение 
. (1.4)
Коэффициенты асимметрии А и эксцесса Е экспоненциального закона распределения равны А =2; Е=6.
Рисунок 1.4 – Экспоненциальное распределение:
а – вероятность безотказной работы, б – плотность вероятности отказа,
в – интенсивность отказов, г – логарифм вероятности безотказной работы.
Характерным признаком экспоненциального распределения является равенство коэффициента вариации единице, т.е.
.
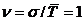Так как интенсивность отказов l = const, то экспоненциальное распределение является распределением без последствий, т.е. вероятность отказов в каждую последующую единицу времени остается неизменной, сколько бы ни проработал безотказно элемент до данного момента времени.
|
|
|
Экспоненциальным законом распределения можно аппроксимировать время безотказной работы широкого круга объектов:
· особо ответственные машины, эксплуатируемые в период после приработки и до существенного проявления постепенных отказов;
· машины с последовательной заменой отказавших деталей;
· электрооборудование; гидроприводы и гидравлическое оборудование;
· системы управления сложных объектов, состоящих из многих элементов и др.; при этом время безотказной работы каждого из них может быть не распределено по экспоненциальному закону.
Достоинством экспоненциального закона распределения является его простота – оно зависит только от одного параметра. Принимая во внимание, что обычно 
, вероятность безотказной работы после разложения в ряд и отбрасывания малых членов ряда можно записать
.
Вероятность безотказной работы в зависимости от величины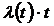 
составит
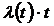1; 0,1; 0,01; 0,001; 0,0001
0,368; 0,9; 0.99; 0,999; 0,9999
Если 
, то вероятность безотказной работы 
, где 
- средняя наработка на отказ. Поэтому 63% отказов возникает за время 
и только 37% отказов возникает позднее. Отсюда следует, что для обеспечения вероятности безотказной работы 0,9 или 0,99 можно использовать только малую долю среднего срока службы (соответственно 0,1 и 0,01).
Если работа изделия происходит при разных режимах, а, следовательно, и вероятность отказов 
(за время работы от 0 до 
) и 
(за время работы от до 
), то в соответствии с теоремой умножения вероятностей
|
|
|
.
Используя экспоненциальный закон распределения и учитывая, что обычно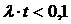 
, можно определить к заданному моменту времени:
· среднее число изделий n, которое выйдет из строя
· среднее число изделий 
, которое останется работоспособным
.
Пример 1.2. Наработка пружины щековой дробилки имеет экспоненциальное распределение со средней наработкой Т = 40 суток. Построить график плотности и функцию данного распределения.
Решение.
Используя формулы (1.1)-(1.4), получим
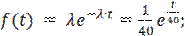
где Q (t)= 1 – P (t) – вероятность отказа.
Результаты расчета приведены на рис. 1.5 и 1.6.
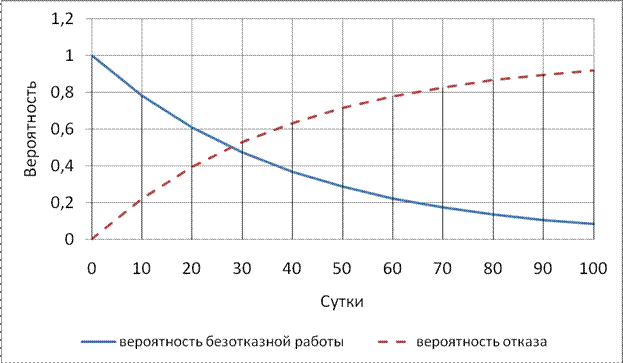
Рисунок 1.5 – Вероятность безотказной работы и отказа для пружины щековой дробилки
Рисунок 1.6 – Плотность вероятности отказов и интенсивность отказов пружины щековой дробилки
Пример 1.7. В конусной дробилке происходят неожиданные отказы футеровочных плит. Определить, в какой момент времени может быть обеспечена вероятность работы P (t) = 0,8, если в межремонтный период t = 30 суток вероятность отказа Q (t) = 0,623.
Решение.
Поскольку отказы происходят внезапно, то предполагаем, что наработки плит описываются экспоненциальным законом. Поэтому значение Q (t) = 0,623 соответствует моменту времени, равному средней наработке Т = 1/λ = 30 суток. Из формулы (1.1) следует
