Распределение Вейбулла

Распределение Вейбулла путем варьирования параметров достаточно универсально охватывает широкий диапазон случаев изменения вероятностей. Оно удовлетворительно описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников и других деталей. Используется для оценки металлургического оборудования, автомобилей, подъемно-транспортных машин и других. Применяется также для оценки надежности по приработочным данным.

Распределение Вейбулла представляет собой двухпараметрическое распределение с плотностью отказов

.

Здесь b - параметр формы, a - ресурсная характеристика.

Вероятность безотказной работы .

Интенсивность отказов .

Средняя наработка .

Дисперсия .

Коэффициент вариации .

Здесь - гамма-функция (определяется по таблицам Приложения Г).

Возможности и универсальность распределения Вейбулла видны из следующих закономерностей:

- при функции и от наработки до отказа убывающие;

- при распределение превращается в экспоненциальное,

т.е. , - убывающая;

- при 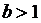функция одновершинная, а функция возрастающая;

- при функция с выпуклостью вверх,

- при функция с выпуклостью вниз;

- при функция линейная и распределение Вейбулла превращается в частный случай, называемый распределением Рэлея;

- при распределение Вейбулла близко к нормальному.

Графическая интерпретация распределения Вейбулла дана на рис. 1.10.

Рисунок 1.10 – Распределение Вейбулла:

а – вероятность безотказной работы, б – плотность вероятности отказа,

в – интенсивность отказов.

Надежность системы, состоящей из последовательно соединенных одинаковых элементов, подчиняющихся распределению Вейбулла, также подчиняется распределению Вейбулла.

Пример 1.11. Наработка питателя барабанной мельницы имеет распределение Вейбулла с параметрами a = 60 суток и b = 1,9. Найти вероятность безотказной работы и интенсивность отказов при наработке Т = 40 суток и определить величину средней наработки на отказ.

Решение.

Подставляя исходные данные в приведенные выше формулы, получим

· вероятность безотказной работы

· интенсивность отказов

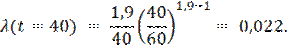
· средняя наработка на отказ

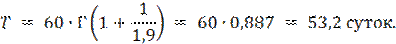
Здесь Г(1+1/1,9) = Г(1,526) = 0,887 – табличное значение гамма-функции (Приложение Г).