Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние много примерно равнозначных факторов. Нормальному закону распределения подчиняются наработки до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры и ошибки измерений и т.п. Нормальное распределение является двухпараметрическим распределением с плотностью
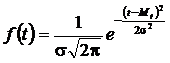 ,
,
где математическое ожидание 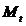 и среднее квадратичное отклонение
и среднее квадратичное отклонение 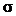 два независимых параметра распределения
два независимых параметра распределения
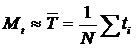 ,
, 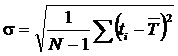 .
.
Для удобства практического использования приведенных зависимостей введем безразмерную переменную u, которая является центрированной 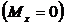 и нормированной (s = 1) величиной и называется квантилем нормированного нормального распределения
и нормированной (s = 1) величиной и называется квантилем нормированного нормального распределения
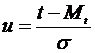
Тогда плотность вероятности и функция распределения при нормальном законе будут иметь так называемый стандартный или нормированный вид.
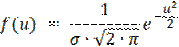
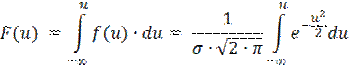
Для вычисления функции плотности нормального распределения f(u) используют таблицы, рассчитанные для плотности нормированного нормального распределения(Приложение Б).
Числовые характеристики нормального закона распределения
Средняя наработка 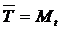 ,
,
Дисперсия 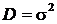 .
.
Коэффициент асимметрии и эксцесс равны нулю, т.е. А = 0, Е = 0.
Графическое представление нормального закона распределения приведено на рис. 1.7.
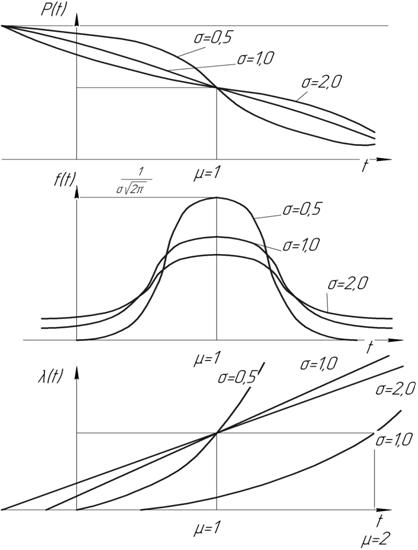
Рисунок 1.7 - Нормальное распределение:
а – вероятность безотказной работы, б – плотность вероятности отказа,
Максимальная ордината кривой равна 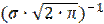 и соответствует точке х = а; по мере удаления от этой точки плотность распределения уменьшается и асимптотически приближается к оси абсцисс при х → ±∞. Так как площадь под кривой распределения всегда равна 1, то при увеличении среднеквадратичного отклонения σ кривая распределения становится более плоской. Поэтому чем больше σ, тем значительнее разброс случайной величины вокруг её среднего значения.
и соответствует точке х = а; по мере удаления от этой точки плотность распределения уменьшается и асимптотически приближается к оси абсцисс при х → ±∞. Так как площадь под кривой распределения всегда равна 1, то при увеличении среднеквадратичного отклонения σ кривая распределения становится более плоской. Поэтому чем больше σ, тем значительнее разброс случайной величины вокруг её среднего значения.
Значения функции распределения F(u) можно найти с помощью таблицы, приведенной в Приложении Б, в которой приведены значения функции Лапласа
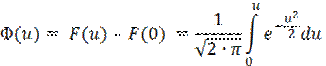
Функция Лапласа Φ(u) является нечетной, т.е. Φ(-u) = -Φ(+u), и поэтому в таблицах даны значения Φ(u) только для u ³ 0. Функция Лапласа имеет следующие свойства
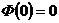 ;
; 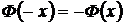 ;
; 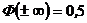 .
.
Функция распределения F(u) выражается через функцию Лапласа Φ(u) следующим образом
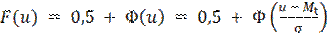
Вероятность того, что распределенная по нормальному закону случайная величина Х примет значение в интервале x1 ≤ X ≤ x2, можно определить по формуле
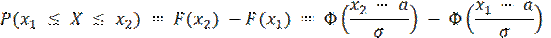
Вычислим вероятность обнаружить отклонение случайной величины Х, распределенной по нормальному закону, от среднего значения a на величину больше σ, 2σ и 3σ. Используя табличные данные, находим
P([a - σ] <X <[a + σ] = Φ(1) - Φ(-1) = 2 Φ(1) = 0,6826;
P([a - 2σ] <X <[a + 2σ] = Φ(2) - Φ(-2) = 2 Φ(2) = 0,9544;
P([a - 3σ] <X <[a + 3σ] = Φ(3) - Φ(-3) = 2 Φ(3) = 0,9972.
Из полученных данных следует, что отклонения случайной величины, распределенной по нормальному закону, от её математического ожидания более чем на 3σ практически невозможны. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигм».
С использованием функции Лапласа вероятность отказов и вероятность безотказной работы будет
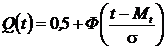 ,
, 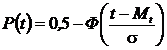 .
.
Значения плотности распределения f(u) и вероятность безотказной работы Q(u) = 0,5 + Ф(u) определяют с использованием таблиц, приведенных в Приложении Б. Например
u 0 1 2 3 4
f(u) 0,3889 0,2420 0,0540 0,0044 0,0001
Q(u) 0,5 0,8413 0,9772 0,9986 0,9999.
Квантиль – числовая характеристика распределения вероятностей. Величину квантиля u P, при котором случайная величина для нормального распределения принимает значение Р (0 £ Р £ 1) можно найти по таблице. приведенной в Приложении В.
Принимая во внимание, что наработки являются неотрицательными величинами, в теории надежности должен использоваться усеченный слева нормальный закон распределения с плотностью (рис. 1.8)
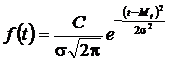 .
.
Здесь коэффициент С определяется через функцию Лапласа Ф
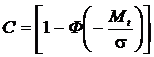 .
.
Например
M t/σ 1 2 3
С 1,189 1,023 1,001.
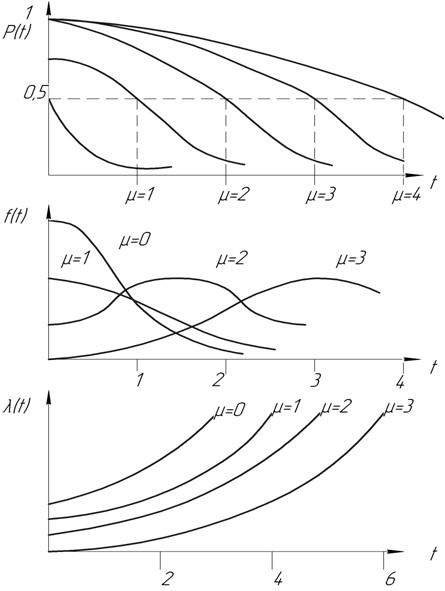
Рисунок 1.8 – Усеченное (слева) нормальное распределение:
а – вероятность безотказной работы, б – плотность вероятности отказа,
Как видно из приведенных данных при M t/σ > 2, коэффициент С @ 1, и поэтому характеристики усеченного нормального распределения практически совпадают с характеристиками нормального распределения.
Вероятность безотказной работы
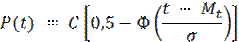
Интенсивность отказов
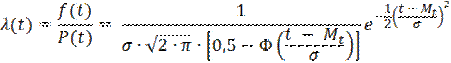
Очевидно, что с увеличением срока эксплуатации интенсивность отказов растет, т.е. снижается надежность изделия. Следует подчеркнуть, что изделия с одинаковой средней наработкой тем лучше, чем меньше величина среднего квадратичного отклонения σ.
Пример 1.8. Футеровки барабанной мельницы имеют наработки, распределенные по нормальному закону с математическим ожиданием M t = 350 суток и средним квадратичным отклонением σ = 50 суток. Найти вероятность безотказной работы футеровок на 300 суток, и определить через какой период времени необходимо произвести их замену, если вероятность появления отказов в процессе эксплуатации не должна превышать 20%.
Решение.
1) Вероятность безотказной работы находим по формуле
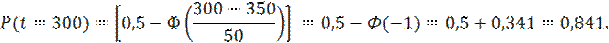
Значение функции Лапласа определено по таблице Приложения Б.
2) По условиям задачи вероятность отказа равна Q(t) = 0,2 и поэтому вероятность безотказной работы P(t) = 1 - Q(t) = 0,8. Табличное значение квантиля u 0,8 = 0,842 (Приложение В). Следовательно, замену футеровки надо проводить через
t = 350 - u 0,8·50 = 350 – 0,542·50 = 308 суток.
Пример 1.9. Наработки шарнира универсального шпинделя описываются нормальным распределением с математическим ожиданием M t = 40 суток и средним квадратичным отклонением σ = 20 суток. Определить, при какой величине M t (если σ = 20 суток) и при какой величине σ (если M t = 40 суток) будет обеспечена в межремонтный период Т = 30 суток вероятность отказа Q(t=30) = 0,1.
Решение.
Заданной вероятности безотказной работы P(t) = 1 - Q(t) = 0,9 соответствует квантиль u 0,9 = 1,28 (Приложение В), и поэтому
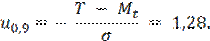
Отсюда
M t = Т + 1,28·σ = 30 + 1,28·20 = 55,6 суток;
σ = - (Т - M t)/ u 0,8= - (30 – 40)/1,28 = 7,8 суток.
Следовательно, для обеспечения вероятности безотказной работы P(t=30)= 0,9, необходимо выполнить одно из следующих мероприятий
1) повысить среднюю наработку плиты с 40 до 55,6 суток, т.е. в 1,4 раза;
2) снизить среднее квадратичное отклонение с 20 до 7,8 суток, т.е. в 2,6 раза.
Повышение средней наработки M t, как правило, связано с большими затратами, направленными на повышение износостойкости (применение новых материалов, разработка более стойких профилей и др.).
Величина среднего квадратичного отклонения σ обычно связана с нарушениями технологии получения материалов, процесса изготовления деталей и правил эксплуатации шпинделя. Поэтому достижение более низких значений σ обусловлено не только чисто техническими мерами, но и организационными мероприятиями.
 2017-12-14
2017-12-14 2146
2146

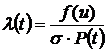 .
.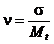 .
.