Средняя наработка до отказа

 

На практике оценить надежность функциональными зависимостями обычно затруднительно, и поэтому надежность элемента характеризуют числовыми характеристиками. Наиболее важными из этих характеристик являются

· среднее время безотказной работы (средняя наработка до отказа) ;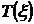

· дисперсия средней наработки до отказа 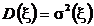, где 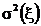- среднее квадратичное отклонение случайной величины .

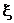Средняя наработка до отказа есть математическое ожидание 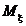случайной величины наработки 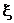, а дисперсия или среднее квадратичное отклонение служит мерой отклонения случайной величины наработки 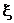от ее математического ожидания 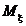,т.е. от средней наработки .

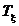Для характеристики степени разброса величины случайной наработки применяют коэффициент вариации, равный отношению среднего квадратичного отклонения к средней наработке .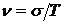

Значение наработки для любого заданного значения 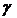в % вероятности безотказной работы получило название гамма-процентной наработки .

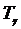Среднее время безотказной работы и среднюю наработку до отказаможно получить по результатам испытаний. Для этого нужно проводить испытания до тех пор, пока не откажет последний из элементов. Пусть время жизни каждого из элементов соответственно равно x ₁, x ₂,..., x _n. Тогда средняя наработка до отказа

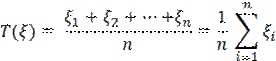
Так как практически невозможно осуществить испытания всех элементов до отказа, то при большом значении п среднюю наработку до отказа можно определить по формуле

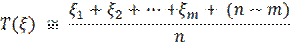
где m — число отказавших элементов, n — число элементов, поставленных на испытания.

Пример 2.3. На испытания поставлено n =100 элементов. Испытания проводились в течение t =200 ч. В процессе проведения испытаний отказало m = 5 элементов, при этом отказы зафиксированы в следующие моменты (часы): x ₁ = 50; x ₂ = 80; x ₃ = 90; x ₄ = 100; x ₅ = 150; остальные элементы не отказали. Определить среднюю наработку до отказа Т(x).

Решение.

Для решения задачи воспользуемся приведенной выше формулой

Т(x) = [(50+80+90+100+150)+(100-5)·200]/100 @ 195 ч.

Пример 2.4. Долговечность комплекта вкладышей шпинделей со стороны валков в линии привода чистовой клети, состоящей из 7 клетей, имеет нормальное распределение с математическим ожиданием M _t = 60 суток и средним квадратичным отклонением s = 10 суток. Определить: 1) возможное число n ₁ вкладышей, которые отказали к моменту времени t ₁ = 50 суток; 2) возможное число n _1,2 вкладышей, которые отказали на интервале времени от t ₁ = 50 суток до t₂ = 60 суток.

Решение.

Число комплектов вкладышей равно N = 14.

Используя нормированную функцию Лапласа, определим вероятность отказа вкладышей к моментам времени t ₁ = 50 суток и t₂ = 60 суток

Q ₁(t = 50) = 0,5 + Ф [(t - M _t)/s] = 0,5 + Ф [(50 – 60)/10] = 0,5 – 0,34 = 0,16.

Q₂ (t = 60) = 0,5 + Ф [(t - M _t)/s] = 0,5 + Ф [(60 – 60)/10] = 0,5 – 0 = 0,50.

Значения функции Лапласа Ф [-1] = – 0,34 и Ф [0] = 0 взято из таблицы (Приложение Г).

Следовательно, возможное число n ₁ вкладышей, которые отказали к моменту времени t ₁ = 50 суток равно

n ₁ = N·Q ₁ = 14·0,159 = 2,23.

Соответственно, возможное число n _1,2 вкладышей, которые отказали на интервале времени от t ₁ = 50 суток до t₂ = 60 суток будет

n _1,2 = N·(Q ₂ - Q ₁)= 14·(0,5 - 0,16) = 4,76.