Допустим на интервале [0, t ] отказ не произошел, и нужно определить вероятность отказа в последующую единицу времени D t (рис. 2.2). Тогда вероятность события С запишется следующим образом (приложение А)
 , или
, или  .
.
Вероятность отказа в промежутке [ t 1, t 2] можно выразить через вероятность безотказной работы


Рисунок 2.2 – Схема к определению вероятности появления события С:
А – событие, в котором на интервале [0, t 1] не произошло отказа;
В – событие, в котором на интервале [ t 1, t 2] произошел отказ;
С – событие, в котором на интервале [0, t 1] не произошло отказа, а на интервале [ t 1, t 2] произошел отказ;
Тогда вероятность того, что в этом интервале произойдет отказ за единицу времени D t = ( ) при условии, что отказа не было до момента времени t1, будет иметь вид
) при условии, что отказа не было до момента времени t1, будет иметь вид
 .
.
Приняв [ t 1, t 2] как [ t 1, t1+Δt ], получим
 .
.
Это соотношение характеризует вероятность отказов за единицу времени на интервале [ t 1, t 2] при условии, что до момента времени t1 отказов не было. Оно получило название интенсивность отказов l. 
Мгновенное значение интенсивности отказов определяется как предел  интенсивности отказов при длине интервала, стремящейся к нулю
интенсивности отказов при длине интервала, стремящейся к нулю

Мгновенное значение интенсивности отказов показывает изменение интенсивности отказов на протяжении срока службы некоторой совокупности объектов (механизмов, узлов, деталей).
Интенсивность отказов связана с вероятностью безотказной работы и плотностью вероятности отказов соотношениями
 ,
,  .
.
Интенсивность отказов, рассматриваемая на каком-то промежутке времени, называется накопленной интенсивностью отказов 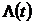 и связана с мгновенным значением интенсивности отказов и вероятностью безотказной работы соотношениям.
и связана с мгновенным значением интенсивности отказов и вероятностью безотказной работы соотношениям.
 ;
; 
Функция λ(t) может быть определена по результатам испытаний. Предположим, что испытаниям подвергают N элементов. Пусть n (t) — число элементов, не отказавших к моменту t. Тогда при достаточно малом Δ t и достаточно большом N получим
λ(t) = Δ n /[Δ t n (t)],
где Δ n — число отказов на участке Δ t.
Статистическая интенсивность отказовλ(t) равна отношению числа отказов, происшедших в единицу времени, к общему числу не отказавших элементов к этому моменту времени.
Многочисленные опытные данные показывают, что для многих элементов функция λ(t) имеет корытообразный вид (рис. 2.3).

Рисунок 2.3 – Изменение интенсивности отказов за период службы изделия.
Из анализа графика следует, что время испытания можно условно разбить на три периода. В первом из них функция λ(t) имеет повышенные значения. Это период приработки или период ранних отказов для скрытых дефектов. Для начального периода [0, t 1] характерны отказы вследствие дефектов материалов, конструкторских недоработок, дефектов изготовления. Этот отрезок кривой получил название период “детской смертности”
Второй отрезок кривой [ t 1, t 2] называют периодом нормальной работы; он отображает случайные внезапные отказы, вызванные неожиданным увеличением нагрузки, предельно тяжелыми условиями работы и т.д. Для этого периода характерна постоянная интенсивность отказов.
Отрезок кривой после t2 характеризует старение объекта, что является следствием, как правило, проявлением отказов, вызванных износом.
Иными словами интенсивность отказов характеризует изменения качества изделия в процессе эксплуатации.
Так как период нормальной работы является основным, то в расчетах надежности принимается λ(t)=λ=const. В этом случае при экспоненциальном законе распределения функция надежности имеет вид (см. п. 1.4):
Р (t) = exp(- λ t).
Среднее время жизни соответственно равно: T 0 = 1/λ. Поэтому функцию надежности можно записать и так:
Р (t) = еxp(- t / T 0).
Если время работы элемента мало по сравнению со средним временем жизни, то можно использовать приближенную формулу
Р (t) ≈ 1 – t / T 0.
Пример 2.1. По данным эксплуатации шестеренной клети установлено, что наработка до отказа подчиняется экспоненциальному закону с параметром λ = 2,10-5 1/час. Найти вероятность безотказной работы за время t = 100 часов. Определить математическое ожидание наработки до отказа.
Решение.
Вероятность безотказной работы
P (t) = exp(- λ· t) = exp(-2,10-5·100) = 0,998.
Математическое ожидание наработки до отказа
M Т = 1/λ = 1/(2,10-5) = 5·104 ч.
Пример 2.2. На испытания поставлено N = 200элементов, испытания проводились в течение t = 100 ч. Построить кривую интенсивности отказов по данным приведенной таблицы: Δ t — интервал испытаний; n — число отказов; (N-n) — число не отказавших элементов.
| № | Δ t | n | N-n | № | Δ t | n | N-n |
| 0…10 | 50…60 | ||||||
| 10…20 | 60…70 | ||||||
| 20…30 | 70…80 | ||||||
| 30…40 | 80…90 | ||||||
| 40…50 | 90…100 |
Решение.
Вычисляем интенсивности отказов на границах интервалов (час-1):
λ(t 1) = 10/(10·190) = 0,0052; λ(t 2) = 8/(10·182) = 0,0044;
λ(t 3) = 6/(10·176) = 0,0034; λ(t 4) = 4/(10·172) = 0,0023;
λ(t 5) = 2/(10·170) = 0,0011; λ(t 6) = 2/(10·168) = 0,0011;
λ(t 7) = 2/(10·166) = 0,0012; λ(t 8) = 4/(10·162) = 0,0024;
λ(t 9) = 5/(10·157) = 0,0032; λ(t 10) = 8/(10·149) = 0,0053.
 |
Рисунок 2.4 – Зависимость интенсивности отказов во времени
Кривая интенсивности отказов приведена на рисунке 2.4.
 2017-12-14
2017-12-14 3688
3688
