Оценивание показателей на основе непараметрических методов

Оценку показателей безотказности возможно получить и тогда, когда не известен вид закона распределения или известно, что распределение относится к классу возрастающей функции интенсивности отказов. В этом случае оценивание осуществляют на основе непараметрических методов, одним из которых является метод множественной оценки показателей безотказности. Начинают с вычисления функции распределения наработок непосредственно с упорядоченной статистической совокупности, в которой наработки до отказа и до цензурирования выстроены в порядке не убывания. Если значения наработки до цензурирования и до отказа равны, то сначала указывают наработку до отказа, а затем наработку до цензурирования.

Для каждой наработки до отказа t_i вычисляют оценки вероятности безотказной работы и вероятность отказа по следующим формулам

- при планах [NUN] и [NUT]

, , N > 10.

, N < 10.

- при плане [NUz]

где - число работоспособных изделий после отказа при наработке .

Точечное оценивание производят по формулам:

- средняя наработка до отказа

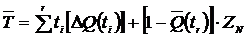где - наработка до отказа, - наработка до цензурирования, , ;

- гамма-процентная наработка

где , ;

- вероятность безотказной работы

, , , ,

Нижняя допустимая граница средней наработки до отказа определяется по формуле .

Пример 4.5. Имеется упорядоченная статистическая совокупность по наработкам (сутки): 4*, 5, 6*, 7, 8, 9, 9, 10, 10*, 12, 12, 12*, 15, 21. Найти точечные оценки вероятности безотказной работы для наработки t = 9 суток, точечную и нижнюю доверительную границу средней наработки до отказа для q = 0,9.

Решение.

Точечную оценку средней наработки до отказа вычисляют по формуле