В ряде случаев условия работоспособности машины можно определить параметрами износа, прочности, нагружения и др. Эти параметры называют определяющими. Модели отказов, использующие определяющие параметры называют параметрическими моделями надежности, а надежность изделий, оцениваемую на основе этих моделей, называют параметрической надежностью.
В этом случае оценка параметрической надежности изделия возможна по результатам измерения определяющих параметров, не дожидаясь появления отказов изделия, и появляется возможность прогноза уровня его надежности.
Частным случаем таких моделей являются допусковые модели, в которых величина определяющего параметра не должна выходить за некоторую допустимую область. Условие работоспособности для таких моделей имеет вид
 ;
;  .
.
Здесь U – определяющий параметр (износ), рассматриваемый в некоторый момент времени на интервале 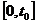 , где t0 – заданная продолжительность функционирования изделия; [ U ] - величина допуска, заданного ТУ; Uд - максимальная допустимая величина износа.
, где t0 – заданная продолжительность функционирования изделия; [ U ] - величина допуска, заданного ТУ; Uд - максимальная допустимая величина износа.
Запись  означает, что событие А состоит в том, что величина износа U находится в допустимой области, ограниченной величиной допуска [ U ], заданной ТУ, и максимальной допустимой величиной износа Uд. Это, так называемая, статистическая (допусковая) модель, в которой точечная оценка вероятности безотказной работы, что величина износа, имеющего нормальный закон распределения, находится по формуле
означает, что событие А состоит в том, что величина износа U находится в допустимой области, ограниченной величиной допуска [ U ], заданной ТУ, и максимальной допустимой величиной износа Uд. Это, так называемая, статистическая (допусковая) модель, в которой точечная оценка вероятности безотказной работы, что величина износа, имеющего нормальный закон распределения, находится по формуле
 ,
,
где 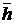 - нормированный допуск, равный
- нормированный допуск, равный  .
.
Нижняя и верхняя доверительные границы безотказной работы определяются по формулам
 ,
,  ,
,
где  - функция Лапласа,
- функция Лапласа,
 ,
,  ,
,
где  - квантиль порядка q, определяемый по таблице (Приложение В).
- квантиль порядка q, определяемый по таблице (Приложение В).
Пример 4.6. Величина зазора подшипника скольжения U по ТУ должна удовлетворять требованиям  , где
, где  мм - допустимая величина зазора в течение наработки t0. По результатам испытаний N=4 подшипников были получены следующие результаты измерения зазоров (в мм):5,4; 6,0; 6,2; 6,4. Оценить вероятность безотказной работы за наработку t0 =30 суток (межремонтный период), если распределение
мм - допустимая величина зазора в течение наработки t0. По результатам испытаний N=4 подшипников были получены следующие результаты измерения зазоров (в мм):5,4; 6,0; 6,2; 6,4. Оценить вероятность безотказной работы за наработку t0 =30 суток (межремонтный период), если распределение  принято нормальным.
принято нормальным.
Решение.
Оценка параметров  и
и  , соответственно равны
, соответственно равны

 .
.
 .
.
Вероятность безотказной работы  .
.
Нижняя доверительная граница вероятности безотказной работы при q=0,9
 .
. 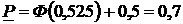 .
.
 2017-12-14
2017-12-14 662
662








