О решении текстовых задач

Высшей категории

МБОУ СОШ №61

Чижова С.А.

 

Иваново 2012

Содержание

Стр.

1. Пояснительная записка______________________________ 3.

2. О решении текстовых задач.__________________________ 4.

3. Задачи на движение.________________________________ 9.

4. Задачи на работу и производительность труда.__________ 17.

5. Задачи на проценты и смеси._________________________ 21.

6. Задачи с целочисленными неизвестными.______________ 34.

7. Задачи с практическим содержанием.__________________ 41.

8. Задачи экологического содержания.___________________ 42.

9. Литература_________________________________________ 48.

 

 

Пояснительная записка

Задачи на составление уравнений или текстовые алгебраические задачи представляют собой традиционный раздел элементарной математики. Интерес к задачам на составление уравнений вполне понятен. Решение этих задач способствует развитию логического мышления, сообразительности и наблюдательности, умения самостоятельно осуществлять небольшие исследования. В текстовых задачах, как правило, речь идёт о конкретных ситуациях из практической деятельности. При их решении выписываются соотношения, представляющие собой математическую модель описанной в задаче практической ситуации. Таким образом, они позволяют проверить не только навыки в решении уравнений и систем уравнений, но и умение описывать с помощью математических соотношений реальные события. Этим и объясняется тот факт, что задачи на составление уравнений являются непременным элементом контрольно - измерительных материалов ЕГЭ.

В работе приводятся методические рекомендации по решению текстовых задач, типы и методы их решения. Некоторые задачи, послужившие примерами к изложенному в работе материалу, заимствованы из контрольно - измерительных материалов ЕГЭ. В конце каждого раздела содержатся задачи для самостоятельного решения, которые помогут проверить, насколько усвоен прочитанный материал.

Работа предназначена для учителей математике и может быть полезна учащимся 9 – 11 классов. Задачи, рассмотренные в данной работе помогут учителю привить интерес учащихся к предмету, расширить их кругозор, активизировать работу на уроке, развить творческое мышление учащихся, подготовить ребят к практической деятельности в любой сфере. Предлагаемые задачи рассчитаны на учащихся различных уровней подготовленности. Это позволит ребятам расширить круг задач, познакомится с нестандартными приёмами решения, научит рассуждать, анализировать, доказывать, преодолевать трудности.

Материалы работы можно использовать на уроках при изучении соответствующих разделов школьной программы, на элективных курсах, при подготовке к ЕГЭ.

 

 

О решении текстовых задач.

Решение текстовых задач играет в математическом образовании очень важную роль. Одним из основных показателей глубины усвоения учащимися учебного материала и уровня математического развития является умение решать задачи, текстовые в том числе

Задачи выступают и целью обучения и его способом. Посредством задач у учащихся формируются математические понятия, исследуются математические законы. Задачи являются средством развития логического мышления, показывают значение математики в повседневной жизни, помогают учащимся использовать полученные знания в практической деятельности.

Ведущие методисты отмечают, что решение текстовых задач преследует двойную цель: с одной стороны – научить решать текстовые задачи различных видов, с другой стороны – сами текстовые задачи выступают как средство обучения, воспитания и развития школьников.

Однако, к сожалению, до сих пор, чаще всего для обучения детей решению задач учителями употребляется лишь показ способов решения определенных видов задач и закрепление их решения механически, хотя решение задач призвано, с первых шагов знакомства с ними, развивать логическое мышление, смекалку, сообразительность; в работе с задачами совершенствуются логические умения проводить анализ и синтез, обобщать и конкретизировать, раскрывать основное, выделять главное в тексте и отбрасывать несущественное, второстепенное; воспитывать личностные качества – терпение, настойчивость, волю.

Нельзя не отметить и тот факт, что часто при решении задач у учащихся также пробуждается интерес к самому процессу поиска решения, при достижении цели дети получают моральное удовлетворение (при правильной организации работы над задачей). При решении задач дети разных возрастов получают новые знания, обобщают и систематизируют полученные ранее.

У учащихся в процессе решения задач происходит формирование различных математических понятий. Используемые в текстовых задачах житейские понятия и представления являются исходным материалом для формирования первоначальных абстракций и математических понятий у учащихся. С другой стороны, такие задачи позволяют учащимся видеть за математическими понятиями и отношениями вполне реальные, жизненные явления.

В системе задач также проводится пропедевтика функциональной зависимости, более глубокое закрепление идеи которой происходит в старших классах.

Решение задач также повышает вычислительную культуру учащихся. В процессе решения текстовых задач у учащихся формируются умения и навыки моделирования реальных объектов и явлений, перевода на математический язык реальных жизненных ситуаций.

В обучении школьников решению задач учителю необходимо обратить внимание на целенаправленное формирование у каждого учащегося следующей структуры умений.

 

Структура умений решать текстовые задачи

Умения	Операционный состав умений
Умение анализировать задачу	- проводить первичный анализ текста (представление задачной ситуации, выделение условия и требования, опорных слов); - выделять известные, неизвестные, искомые величины; - устанавливать связи между данными и искомыми; - конструировать модели задачной ситуации (предметные, схематические, графические) и соотносить элементы задачи с элементами модели; - устанавливать полноту данных задачи (достаточность, недостаточность, избыточность); - узнавать типы задач
Умение проводить поиск плана решения задачи	- раскладывать составную задачу на простые; - переводить зависимость данных и искомых на математический язык; - выбирать рациональные способы решения задач; - проводить рассуждения аналитическим и синтетическим способом; - активизировать необходимые для решения задачи теоретические знания
Умение реализовать найденный план решения задачи	- устанавливать адекватность построенной математической модели исходной задаче; - рационально выбирать математические связи между величинами; - устанавливать соответствие промежуточных и конечного результатов; - оформлять решение
Умение осуществлять контроль и коррекцию решения	- определять соответствие полученных результатов исходной задаче; - выполнять проверку решения разными способами; - находить другие способы решения задачи; - оценивать полученные при решении результаты; - обобщать результаты решения.

 

 

Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.

Для решения текстовых задач применяются три основных метода: арифметический, алгебраический и комбинированный. Рассмотрим каждый из этих методов.

I. Арифметический метод.

Первым этапом решения задач арифметическим методом является разбор условия задачи и составление плана её решения. Этот этап решения задачи сопровождается максимальной мыслительной деятельностью.

Вторым этапом является решение задачи по составленному плану. Этот этап решения проводится учащимися без особых затруднений и в большинстве случаев носит тренировочный характер.

Третьим важным этапом решения задачи является проверка решения задачи. Она проводится по условию задачи. Пренебрежение проверкой при решении задачи, замена её проверкой ответов снижает роль решения задачи в процессе развития логического мышления учащихся.

II. Алгебраический метод.

Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или системы неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.

При решении задач алгебраическим методом основная мыслительная деятельность сосредотачивается на первом этапе решения задачи: на разборе условия задачи и составлении уравнений или неравенств по условию задачи.

Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств.

Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.

III. Комбинированный метод.

Этот метод получается в результате того, что часть неизвестных величин определяется с помощью решения уравнения или системы уравнений, неравенств или систем неравенств, а другая часть – арифметическим методом. В этом случае решение текстовых задач значительно упрощается.

При решении текстовых задач учащимся могут помочь несколько простых и общих советов, а также приведённые ниже примеры решения задач.

Совет 1. Не просто прочитайте, а тщательно изучите условие задачи. Попытайтесь полученную информацию представить в другом виде – это может быть рисунок, таблица или просто краткая запись условия задачи.

Совет 2. Выбор неизвестных.В задачах "на движение" – это обычно скорость, время, путь. В задачах “на работу” - производительность и т.д.

Не надо бояться большого количества неизвестных или уравнений. Главное, чтобы они соответствовали условию задачи и можно было составить соответствующую “математическую модель” (уравнение, неравенство, система уравнений или неравенств).

Совет 3. Составление и решение “математической модели”.При составлении “математической модели” (уравнения, неравенства, системы уравнений или неравенств) ещё раз внимательно прочитайте условие задачи. Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый “знак” полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).

Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить составленное.

Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и полученную запись). Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации.

Если кажется, что получилось правильное, но очень сложное выражение, то попробуйте ввести другие неизвестные, может быть, изменив их количество, чтобы получилась более простая модель.

Иногда неизвестные в задачах выражаются только целыми числами, тогда при решении задач нужно использовать свойства целых чисел.

Совет 4. Решение сложной текстовой задачи – процесс творческий. Иной раз требуется вернуться к самому началу задачи, учитывая и анализируя уже полученные результаты.

При решении задач короткую запись задачи можно сделать с помощью рисунка или таблицы.

Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.

Можно выделить семь вопросов, которые дают верное направление решению задач разных типов.

Вопросы к задаче с комментариями к ним:

О каком процессе идёт речь? Какими величинами характеризуется этот процесс? (Количество величин соответствует числу столбцов таблицы).

Сколько процессов в задаче? (Количество процессов соответствует числу строк в таблице).

Какие величины известны? Что надо найти? (Таблица заполняется данными задачи; ставится знак вопроса).

Как связаны величины в задаче? (Вписать основные формулы, выяснить связи и соотношения величин в таблице).

Какую величину (величины) удобно выбрать в качестве неизвестной или неизвестных? (Клетки в таблице заполняются в соответствии с выбранными неизвестными).

Какие условия используются для составления “модели”? (Выписать полученную “модель”)

Легко ли решить полученное? (Если решить сложно, ввести новые переменные, использовать другие соотношения).

Задачи на движение.

 

Обычно в задачах на движение, если не оговорено дополнительно, используются следующие допущения: движение на отдельных участках считается равномерным, повороты считаются мгновенными, т. е. без затрат времени, скорость при этом меняется мгновенно.

В качестве переменных принимаются величины S – путь или расстояние, V – скорость, t – время.

При решении задач на движение полезно сра­зу переводить все данные в одни и те же едини­цы измерения.

Пример 1. На путь между двумя деревнями пе­шеход затратил на 4 ч 30 мин больше, чем мо­тоциклист. Скорость мотоциклиста 40 км/ч, скорость пешехода составляет 1/10 скорости мотоцик­листа. Найдите расстояние между деревнями.

Решение. Во-первых, найдем скорость пе­шехода. Она равна 4 км/ч.

Пусть мотоциклист может проехать расстояние между деревнями за х ч, тогда пешеход может пройти это расстояние за (х + 4,5) ч. Таким об­разом, пешеход пройдет 4(х + 4,5) км, мотоцик­лист проедет 40х км.

Так как по условию задачи эти величины рав­ны, получим уравнение

4(х + 4,5) = 40х, откуда х = 0,5.

Следовательно, расстояние между деревнями равно 0,5 * 40 = 20 (км).

Ответ: 20.

В следующих задачах запланированные параме­тры движения (расстояние, время и скорость) со­поставляются с реальными.

Для решения подобных задач необходимо вы­разить через переменную расстояние, время и скорость на каждом из запланированных и реаль­ных участков пути с момента отклонения от пла­на. После этого нужно найти в условии задачи еще не использованный факт и с его помощью составить уравнение.

Пример 2. Велосипедист должен был проехать весь путь с определенной скоростью за 2 ч. Но он ехал со скоростью, превышающей намеченную

на 3 км/ч, и поэтому на весь путь затратил 5/3 ч.Найдите длину пути.

Решение. При решении этой задачи полез­но рассматривать как бы два участка пути — за­планированный и реальный. Они, естественно, равны по длине, но отличаются временем и ско­ростью их прохождения.

По плану: затраченное время 2 ч, скорость обозначим х км/ч, расстояние равно 2х км.

В реальности: скорость (х + 3) км/ч, время 5/3 ч, значит, расстояние равно 5/3(х + 3) км.

Поскольку в реальности пройдено именно то расстояние, которое и было запланировано, по­лучаем уравнение 2х=5/3(х+3),откуда х = 15.

Итак, велосипедист должен был за 2 ч со ско­ростью 15 км/ч проехать расстояние 2 • 15 = 30 км Ответ 30.

Пример 3. Автобус прошел 5/6 пути со скоростью 50 км/ч, а затем задержался на 3 мин. Что­бы прибыть в конечный путь вовремя, оставшу­юся часть пути он шел со скоростью 60 км/ч. Найдите путь, пройденный автобусом.

Решение. Отклонение от плана началось с момента остановки. Обозначим за х ч — время, за которое автобус должен был пройти оставшуюся 1/6 часть пути. Тогда запланированное расстояние равно 50х км.

В реальности 1/20 ч автобус стоял, а оставшуюся часть пути прошел за(х-1/20) ч, то естьреально пройденный путь равен 60 (х-1/20) км.

По условию задачи запланированное расстояние совпадает с реально пройденным, следовательно, получаем уравнение60(х-1/20) = 50х, откуда х = 0,3. Таким образом, 1/6 часть пути равна 50 • 0,3 = 15 (км), а весь путь равен 15 • 6 = 90 (км).О т в е т: 90.

Рассмотрим задачи, описывающие движение двух участников. В задачах на совместное движе­ние участники не всегда одновременно начинают движение и не всегда одновременно его заканчи­вают. Поэтому очень важно выделить участок или участки пути, на которых движение происходит действительно совместно. Кроме этого, в задачах имеются, как правило, такие участки пути, на ко­торых передвигается один участник, в то время как другой еще не начал или уже закончил дви­жение.

В некоторых задачах полезно найти скорость сближения (или удаления) участников — величи­ну, показывающую, на сколько уменьшается (или увеличивается) расстояние между участниками движения в единицу времени.

Замечания.

Скорость сближения или удаления равна сум­ме скоростей участников при их движении в про­тивоположных направлениях (навстречу друг дру­гу или друг от друга).

При движении участников в одном направлении (один убегает, другой его догоняет) скорость сбли­жения или удаления равна модулю разности их скоростей.

Пример 4. Из Смоленска в Москву вышел по­езд со скоростью 70 км/ч. Спустя 1 ч 40 мин из Москвы в Смоленск отправился поезд, скорость которого равна 60 км/ч. Через сколько часов по­сле выхода поезда из Смоленска произойдет встреча, если расстояние между городами равно 420 км?

Решение. Совместное движение началось в момент выхода из Москвы первого поезда. К этому времени второй поезд прошел 70 •5/3=350/3(км) и расстояние между поездами сократилось до

420-350/3=910/3 (км).

Закончилось совместное движение их встречей.

Итак, на расстоянии 910/3 (км) поезда сбли­жались со скоростью 70 + 60 = 130 (км/ч) и потратили на это

910/3:130=7/3 (ч)

Тогда поезд из Смоленска шел до встречи 5/3 + 7/3 = 12/3= 4 (ч).

О т в е т: 4.

В ряде задач на движение учитываются ско­рость ветра при движении самолетов, скорость течения при движении по реке. В задачах такого типа рассматриваются две основные скорости - собственная скорость самолета, корабля, лодки, создаваемая двигателем или усилием людей при работе на веслах, т.е. скорость движения при от­сутствии ветра или в стоячей воде, и скорость ветра или течения. Как правило, если собствен­ная скорость и скорость ветра (или течения) не даны, то именно их обозначают переменными. Две другие скорости — скорость по ветру или те­чению и скорость против ветра или течения — можно выразить через основные скорости (через их сумму или разность). Далее решаем задачу, как любую другую задачу на движение.

Пример 6. Самолет пролетит по направлению ветра за 5,5 ч такое же расстояние, какое в об­ратном направлении за 6 ч при условии, что ни скорость, ни направление ветра не меняются. Найдите расстояние, которое пролетит самолет туда и обратно, если собственная скорость само­лета равна 690 км/ч.

Решение. В данной задаче основные скоро­сти — собственная скорость самолета, равная 690 км/ч, и скорость ветра, которая не дана. Обозначим ее за х км/ч.

Тогда при движении по направлению ветра са­молет со скоростью (690 + х) км/ч за 5,5 ч про­летит 5,5(690 + х) км, а при движении против направления ветра самолет со скоростью (690 - х) км/ч за 6 ч пролетит 6(690 - х) км.

Учитывая, что по условию задачи самолет туда и обратно пролетает одно и то же расстояние, со­ставим уравнение

5,5 • (690 + х) = 6 • (690 - х).

Решая уравнение, находим, что скорость ветра равна 30 км/ч. Далее вычислим расстояние: 6 • (690 - 30) = 3960 (км).

Туда и обратно самолет пролетит 3960 • 2 == 7920 (км).

Ответ: 7920

Пример №7 Из города выехал грузовик со скоростью 60 км/ч. Через 2 часа вдогонку выехал мотоциклист. В некоторый момент времени расстояние между ними было 80 км. Если бы скорость мотоциклиста была в 5/4 раза больше, чем в действительности, то это расстояние оказалось бы в три р а за меньше. Найти скорость мотоциклиста.

Решение: Пусть скорость мотоциклиста v км/ч, а t – время до момента, когда расстояние

между ними впервые стало равно 80 км. Тогда за время t ч грузовик прошел расстояние

60t км, а мотоциклист за время t - 2 проехал v(t - 2) км. Откуда получаем уравнение

Аналогично из второго условия вытекает второе уравнение

Таким образом, получаем систему уравнений

Вычитая теперь из первого уравнения второе и умножая затем обе части полученного уравнения на 4, приходим к соотношению

Теперь из первого уравнения следует t = 44/9, следовательно,

v = 960/13 = км/ч.

Ответ: км/ч.

Пример №8 Два самолета вылетели одновременно из пунктов A и B навстречу друг другу и встретились на расстоянии 100 км от середины AB. Если бы первый самолет вылетел на 20 минут позже второго, то они встретились бы на четверти пути от A, а если бы второй самолет вылетел на 20 минут позже первого, то они встретились бы на полпути. Определить скорости самолетов.

Решение:

Пусть скорости первого и второго самолетов равны соответственно V1 и V2 км/ч, а расстояние между A и В – S км.

Для составления системы уравнений составим таблицу:

Условия задачи	Уравнения
Если бы первый самолет вылетел на 20 минут позже второго, то они встретились бы на четверти пути от А.
Если бы второй самолет вылетел на 20 минут позже первого, то они встретились бы на полпути.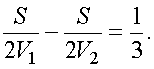

 

Заметим, что как видно из второго уравнения V2 > V1 т.е. первое условие задачи позволяет заключить:

Самолеты встретились на расстоянии 100 км от середины АВ.

Таким образом, приходим к системе уравнений

Откуда S = 800 км, км/ч, км/ч.

Пример№9 Грузовой и легковой автомобили выехали одновременно навстречу друг другу соответственно из пунктов А и В. После встречи грузовой автомобиль прибывает в В через два часа, а легковой в А через 9/8 часа. Каждый едет с постоянной скоростью без остановки и, приехав в конечный пункт, тут же поворачивает обратно, и на обратном пути встречаются в 60 км от В. Найти время затраченное каждым автомобилем на поездку туда и обратно.

Решение: Пусть скорость грузового автомобиля V1 км/ч, скорость легкового автомобиля V2 км/ч, а расстояние от А до В равно S км.

 

Тогда имеем:

первая встреча грузовика и легкового автомобиля

 

Следовательно, получаем первые два уравнения:

Условия задачи	Уравнения
После встречи грузовой автомобиль прибывает в B через 2 ч, легковой автомобиль в А через 9/8 ч.

Для получения второго уравнения рассмотрим второе условие:

вторая встреча грузовика и легкового автомобиля

Приехав в конечный пункт, они тут же поворачивают обратно, и на обратном пути встречаются в 60 км.

Итак, приходим к системе уравнений:

По условию задачи нам необходимо найти величины:

Однако удается определить и остальные переменные

Ответ:

 

Задания для самостоятельной работы.

 

Задание 1. Почтальон проехал на мотоцикле от почты до села со скоростью 30 км/ч. Назад он возвращался пешком со скоростью, составляю­щей 1/5 скорости его движения на мотоцикле,

поэтому на обратный путь он затратил на 1 ч 12 мин больше, чем от почты до села. Найдите расстояние от почты до села.

Задание 2. Расстояние между деревней и по­селком мотоциклист проезжает на 0,4 ч быстрее велосипедиста. Скорость мотоциклиста 18 км/ч,а скорость велосипедиста составляет 8/9 скорости

мотоциклиста. Найдите расстояние между дерев­ней и поселком.

Задание 3. Велосипедист каждую минуту про­езжает на 800 м меньше, чем мотоциклист, поэтому на путь в 30 км он затратил времени на 2 ч больше, чем мотоциклист. Сколько километров в час проезжал мотоциклист?

Задание 4. Путь от А до В пешеход проходит за 2 ч. Если он увеличит скорость на 2 км/ч, то уже за 1,8 ч он пройдет на 3 км больше, чем расстояние от А до В. Найдите расстояние от А до В.

Задание 5. Расстояние между двумя пунктами поезд проходит по расписанию с намеченной ско­ростью за 6 ч. Через 5 ч после отправления он был задержан в пути на 12 мин. Поэтому, чтобы прибыть на станцию назначения вовремя, поезд увеличил скорость на 15 км/ч. Найдите перво­начальную скорость поезда.

Задание 6. Расстояние между двумя пункта­ми автомобиль должен был проехать за 4 ч. Первые 2 ч он ехал с намеченной скоростью, а затем снизил ее на 10 км/ч, поэтому в конеч­ный пункт приехал на 20 мин позже, чем пред­полагал. Найдите первоначальную скорость ав­томобиля.

Задание 7. Расстояние между двумя пунктами автомобиль должен был пройти за 3 ч. Первые 2 ч он ехал с намеченной скоростью, а затем увеличил ее на 10 км/ч, поэтому в конечный пункт приехал на 12 мин раньше, чем предпо­лагал. Найдите расстояние между этими пунк­тами.

Задание 8. Из Москвы в Киев вышел поезд со скоростью 80 км/ч. Спустя 24 мин из Киева в Москву отправился поезд со скоростью 70 км/ч. Через сколько часов после выхода из Москвы про­изойдет встреча, если расстояние между города­ми равно 872 км?

Задание 9. Из города А в город В выехал грузовик со скоростью 45 км/ч. После того как грузовик проехал 15км, из города А выехал со скоростью 60 км/ч автомобиль, который при­ехал в город В на 1/6 ч раньше грузовика. Найдите расстояние между городами.

Задание 10. Расстояние между городами А и В равно 50 км. Из города А в город В выехал велосипедист, а через 1 ч 30 мин вслед за ним выехал мотоциклист. Обогнав велосипедиста, он прибыл в город В на 1 ч раньше его. Найдите скорость мотоциклиста, если известно, что она в 2,5 раза больше скорости велосипедиста.

Задание 11. Из двух пунктов А и В, рассто­яние между которыми равно 5 км, одновремен­но в одном направлении выехали велосипедист и легковой автомобиль. Легковой автомобиль все

время был впереди велосипедиста, и через 2/3 ч. расстояние между ними стало 35 км. Найдите скорость велосипедиста, если она в 4 раза мень­ше скорости легкового автомобиля.

Задание 12. Из двух аэропортов, расстояние между которыми равно 1300 км, вылетели одно­временно навстречу друг другу два самолета — один с поршневым, другой с реактивным двига­телем. Через 30 мин им оставалось пролететь до встречи 800 км. Найдите скорость самолета с реактивным двигателем, если она в 3 раза больше скорости самолета с поршневым двига­телем.

Задание 13. Два туриста отправились одновре­менно из пунктов Аи В, расстояние между которыми равно 33 км, навстречу друг другу. Через 3 ч 12 мин расстояние между ними сокра­тилось до 1 км (они еще не встретились), а еще через 2 ч 18 мин первому осталось пройти до пункта В втрое большее расстояние, чем второму до пункта А. Найдите скорость второго туриста.

Задание 14. Лодка проплывет за 3 ч по тече­нию такое же расстояние, какое за 4 ч против течения. Найдите расстояние, которое проплы­вет лодка вниз по течению, если собственная скорость лодки 14 км/ч.

Задание 15. Из пункта А вниз по течению реки движется лодка с собственной скоростью 17 км/ч. Ей навстречу из пункта В движется катер с соб­ственной скоростью 26 км/ч. Лодка до встречи шла 2 ч, катер — 1,5 ч. Какое расстояние проплывет за 3 ч плот, если расстояние между пунк­тами А и В равно 74 км?

Задание 16. Катер, собственная скорость ко­торого равна 21 км/ч, прошел вниз по реке от города А до города В 72 км и вернулся обрат­но. За это же время пустая канистра, упавшая с борта катера при отходе из города А, проплыла 21 км. Сколько времени понадобится канистре, чтобы доплыть от города А до города В?

Задание 17. Самоходная баржа, собственная скорость которой равна 20 км/ч, прошла по реке от одной пристани до другой 96 км и вернулась обратно. За это же время плот проплывет 40 км. Найдите время движения лодки вверх по реке.

Задание 18. Друзья отправились на пикник на лодке, а вечером вернулись обратно. Они проплы­ли в общей сложности 48 км, затратив на это 2 ч 48 мин. При этом на каждые 3 км против течения им приходилось тратить столько же вре­мени, сколько на 4 км по течению. Найдите соб­ственную скорость лодки.