Задачи с целочисленными неизвестными

Пример №1

Группа студентов решила купить магнитофон ценой от 170 до 195 рублей. Однако в последний момент двое отказались участвовать в покупке, и каждому пришлось внести на 1 рубль больше. Сколько студентов участвовало в покупке?

Решение: Пусть x рублей – стоимость магнитофона, y – первоначальное число студентов. Тогда каждому студенту пришлось затратить 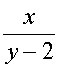рубля, а предполагалось 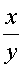рублей, что на 1 рубль меньше. Откуда следует уравнение 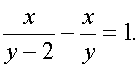Выразим из этого уравнения y через x, решив для этого его как квадратное уравнение, 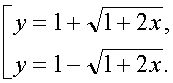Второе соотношение по смыслу не удовлетворяет условию задачи, т.к. число студентов – натуральное число.

С другой стороны, т.к. 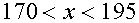, то для y имеем соотношение 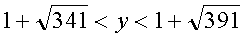.В этих пределах находится лишь одно натуральное число .

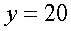Ответ: первоначальное число студентов составило 20 человек, а участвовали в покупке 18, при этом магнитофон стоил 180 рублей.

Пример №2

При подведении итогов работы бригады за месяц вычислено, что процент числа членов бригады перевыполнивших намеченный план, составляет от 92,5 % до 93,5 %. Определить минимальное возможное число членов бригады.

Решение: Пусть в бригаде работает n – человек, а среди них k – перевыполнивших план. Тогда по условию задачи имеет место система неравенств 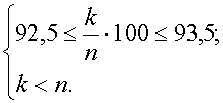Откуда получаем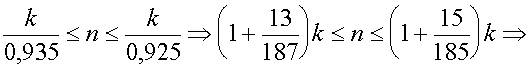 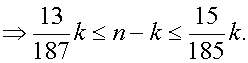Из последнего неравенства легко видно, что, начиная с k = 13, выражение n - k больше 1, т.е. наименьшее n, которое удовлетворяет условиям задачи, равно 14.

Ответ: наименьшее возможное число членов бригады – 14 человек.

Пример №3.

Как набрать сумму 146 руб. из 20 купюр достоинством 1, 3, 5, 10 рублей, если число “пятирублевок” больше числа “трехрублевок” и не больше “десятирублевок” (предполагается, что в набираемой сумме должны присутствовать купюры всех достоинств).

Решение: Пусть x, y, z, t – число купюр достоинством 1, 3, 5, 10 рублей соответственно.

Тогда 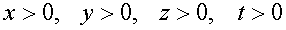, и имеет место система

Вычитая из второго уравнения системы первое, получим 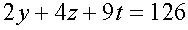, (2)

откуда видим, что t– четное число. С другой стороны, применяя неравенство системы к уравнению (2) и учитывая, что, 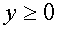получаем 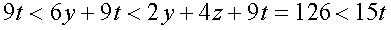. Таким образом, 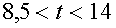. И т.к. t– целое, четное, то возможны лишь два случая t=10,12. При 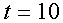система (1) принимает вид 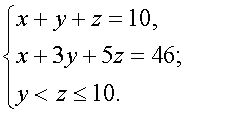Откуда, также как и выше, получаем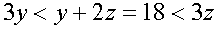

Следовательно, y – четное и z > 6, а y < 6, т.е. для y возможны лишь два случая y = 2,

y = 4.

При y = 2 из уравнения y + 2z = 18 вытекает z = 8, что невозможно, т.к. y + z должно быть меньше 10.

При y = 4 получаем z = 7, что невозможно, т.к. y + z должно быть меньше 10.

Исследуем случай t = 12. Имеем из системы (1) .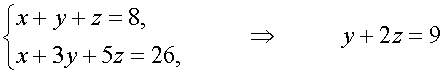

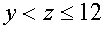Откуда видно, что y – нечетное, причем 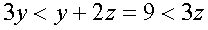.т.е. y < 3 и, значит, y = 1, но тогда z = 4, а x = 3.

Ответ: купюр по 1 рублю – 3, по 3 рубля – 1,

Пример№4.

Имеется некоторое количество проволоки. Если её намотать на катушки, на которые помещается 800 метров проволоки, то одна катушка будет намотана не полностью. То же самое произойдет, если пользоваться только катушками, на которые помещается 900 метров проволоки, причем таких катушек понадобится на три меньше. Если же проволоку наматывать на катушки, на которые помещается 1100 метров, то таких катушек понадобится ещё на шесть меньше, но при этом все такие катушки будут намотаны полностью. Сколько метров проволоки было?

Решение: Обозначим через l искомое число метров проволоки, n – число катушек вместимостью 800 метров.

Тогда имеем систему: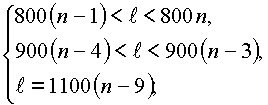

Откуда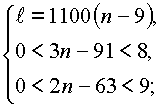

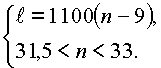
Так как n – натуральное, то n = 32 и l = 25300.

Ответ: 25300 метров.

Пример №5. Подданные привезли в дар шаху 300 драгоценных камней: в маленьких шкатулках по 15 штук в каждой и в больших – по 40 штук в каждой. Сколько было тех и других шкатулок. Если известно, что маленьких было меньше, чем больших?

Решение: Решим в целых числах уравнение:

7х – 11у = 36.

Это линейное уравнение с двумя переменными. Выразим из этого уравнения ту переменную, коэффициент при которой по модулю меньше,

т. е. переменную х: х =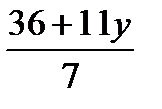

Выделив целую часть, получим: х = 5 + у +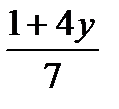

Чтобы значение дроби было целым числом, надо, чтобы 1 + 4у было кратно 7, т. е. 1 + 4у = 7z, где z – целое число.

Мы получили новое уравнение с двумя переменными, коэффициенты которого по модулю меньше коэффициентов первого уравнения. Будем продолжать таким же образом и выразим из него переменную у:

у = 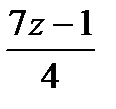= z – 1 + .

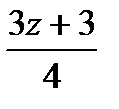Потребуем, чтобы 3z + 3 было кратно 4, т. е. чтобы выполнялось условие 3z + 3 = 4u, где u– целое число. Отсюда

z = 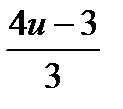= u – 1 + .

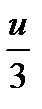Теперь потребуем, чтобы u было кратно 3:

u = 3v,

где v – целое число.

Дробей больших нет. «Спуск» закончен, и надо «подняться вверх», выразив х и у через v. Итак:

z = 4v – 1,

y = 7v – 2,

x = 11v + 2.

Таким образом, х = 11v + 2, у = 7v – 2. Придавая в этих равенствах переменной v целые значения, будем получать целые решения нашего уравнения. Очевидно, что их будет бесконечное множество. Если требуется найти натуральные решения, то надо наложить дополнительное условие:

11v + 2 > 0 и 7v – 2 > 0.

Ответ: 4 маленьких и 6 больших.

Пример №6 Можно ли двухрублевыми и пятирублевыми монетами набрать сумму в 51 рубль. Если да, то сколькими способами.

Решение: Решите в целых числах уравнение:

а) 5х + 12у = 71;

б) 8х – 25у = 11.

Выясните, имеет ли каждое из них натуральные решения.

Выясняем, что и в первом и во втором уравнении целесообразно выразить переменную х через у, так как коэффициент при этой переменной по модулю меньше, чем коэффициент при переменной у. тоговые формуИтоговые формулы у разных учащихся могут быть различными – это связано с тем, что они могут по – разному провести преобразования. Чтобы проверить себя, полезно найти по полученным формулам какое–нибудь целое решение уравнения (например, при v = 0) и подставить его в исходное уравнение. Полезно также для демонстрации эффективности полученных формул предложить учащимся найти по ним несколько целых решений и убедиться, что они действительно удовлетворяют исходному уравнению.

а) Последовательно выражая переменные из получаемых уравнений и двигаясь затем «обратным ходом», можем получить выражения для х и у:

х = 12v + 7, у = 3 – 5v, где v – целое число.

Чтобы выяснить, имеет ли уравнение натуральные решения, решим систему неравенств: 12v + 7 > 0 и 3 – 5v> 0. Получим - 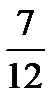<v< 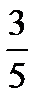. В этом промежутке находится только одно целое значение v, равное 0, значит, уравнение имеет единственное решение в натуральных числах. Оно может быть найдено из полученных формул: при v = 0 имеем х = 7, у = 3.

б) Здесь «спуск» закончится очень быстро – на втором шаге получаем

у = 8z – 3, z - целое число. Отсюда х = 25z – 8, z - целое число. Решив далее систему неравенств 8z – 3 > 0 и 25z – 8 > 0, получим z> 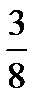, т. е. при целых значениях z, больших или равных 1, мы будем получать натуральные решения. Очевидно, что их бесконечное множество.