Проекции единичных векторов 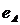 и
и 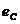 соответствующих осей шарниров А и С на оси системы координат
соответствующих осей шарниров А и С на оси системы координат 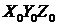 описываются матрицами:
описываются матрицами:
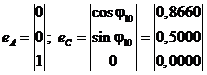 . (1)
. (1)
Для звена 1 определяем векторы углового ускорения и соответствующую матрицу:
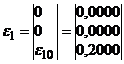 (2)
(2)
Для звена 2 угловое ускорение определяем с помощью векторного уравнения:
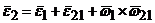 , (3)
, (3)
а так как 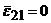 , то получим
, то получим 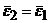 .
.
Вектор относительного углового ускорения, характеризующего закон вращения звена 3 относительно звена 2, определяют по формуле:
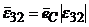 ,
,
а соответствующая матрица записывается в виде:
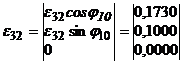 (4)
(4)
Для определения углового ускорения 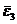 третьего звена составляем векторное уравнение:
третьего звена составляем векторное уравнение:
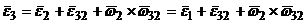 (5)
(5)
В эти уравнения входит векторное произведение 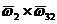 которое, как и произведение любых двух векторов
которое, как и произведение любых двух векторов 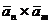 , описываемых матрицами:
, описываемых матрицами:
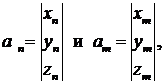 (6)
(6)
в общем виде превращается в вектор с матрицей:
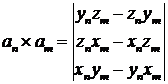 . (7)
. (7)
Подставляя (3) и (4) в (7), получим матрицу-столбец вектора 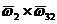 :
:
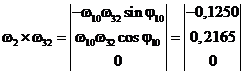 . (8)
. (8)
Подставив (1), (2) и (8) в (5), определяем матрицу:


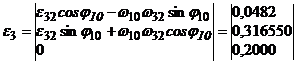 (9)
(9)
а по ним – модуль вектора углового ускорения: 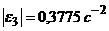 .
.
 2017-12-14
2017-12-14 356
356








