Метод простой итерации

 

Пусть дана система линейных уравнений:

 

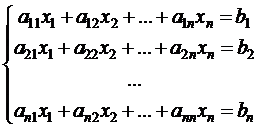. (3.3)

 

 

В матричном виде:

 

,

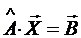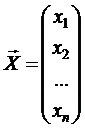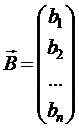; ; . (3.4)

 

Предполагая, что диагональные элементы a_ii ¹ 0,(j = 1, 2, …, n), выразим х ₁ через первое уравнение системы, х ₂ – через второе, и т.д.

 

;

;

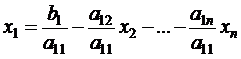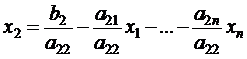… (3.5)

.

 

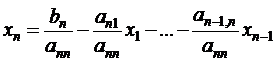Обозначим 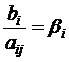, , 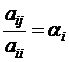где i = 1, …, n; j = 1, …, n, тогда

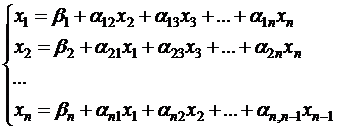(3.6)

 

Эта система называется системой, приведенной к нормальному виду.

 

Введя обозначения

, .

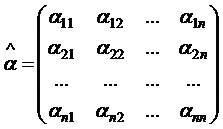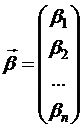Запишем систему (3.3) в матричной форме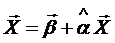

или

. (3.7)

 

Решим систему (3.7) методом последовательного приближения, за нулевое приближение возьмем столбец свободных членов:

 

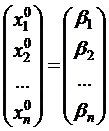- нулевое приближение;

 

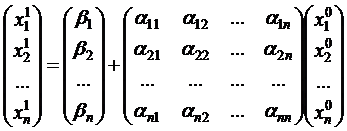- 1-е приближение;

 

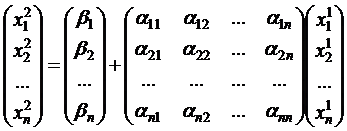- 2-е приближение.

 

Любое приближение вычисляется по формуле X ^{( k+ 1)} = b + aХ ^{( k )}. Если последовательность приближения X ⁽⁰⁾, X ⁽¹⁾, …, X ^{( k )} имеет предел X = lim X ^{( k )} при k 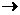¥, то этот предел является решением системы (3.6). Поскольку по свойству предела lim X ^{( k +1)} = b + a lim X ^{( k )}, k 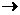¥, тогда X = a + bХ.