Общая характеристика задач электростатики и методов их решения

В зависимости оттого, что задано и что определяется, задачи электростатики могут быть разделены на следующие три типа задач. Задача первого типа: по заданному закону распределения потенциала в пространстве j(х,у,z) найти распределение свободных зарядов, вызвавших поле. Такого рода задачи могут быть решены при помощи уравнения Пуассона. Это наиболее простой тип задач; 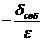в данной точке поля, согласно уравнению Пуассона, равняется сумме частных производных второго порядка от j, в которую подставляются координаты данной точки поля.

Задача второго типа: задан закон распределения свободных зарядов в пространстве в функции координат ρ_свб(х,у,z). Найти закон изменения потенциала в пространстве j_свб (х, у, z). Эта задача является обратной к первой и значительно сложнее ее. Принципиально задача состоит в решении уравнения Пуассона относительно j, т. е. в решении дифференциального уравнения второго порядка в частных производных.

Задачи первого и второго типов практически встречаются редко. В подавляющем большинстве приходится иметь дело с задачами третьего типа.

Задача третьего типа: известны потенциалы (или полные заряды) и геометрия тел, создающих поле. Требуется найти закон изменения Е или j во всех точках поля.

Если среда, в которой создано поле, является неоднородной, то она подразделяется на однородные области и решение уравнения Лапласа производится для каждой области в отдельности. Основная трудность задачи состоит в том, что хотя полные заряды тел и известны, но с какой плотностью на отдельных участках заряженного тела распределены заряды неизвестно. Решения уравнения Лапласа для отдельных областей должны быть согласованы друг с другом: на границе раздела двух сред с различными e должны выполняться граничные условия. На грани раздела проводящего тела и диэлектрика также должны выполняться свои граничные условия. Задачи, отнесенные к группе задач третьего типа, могут быть решены аналитическим или графическим путями, либо путем электромоделирования.

В данном параграфе дадим этим методам (путям решения) лишь краткую характеристику с тем, чтобы читатель составил некоторое предварительное впечатление о тех методах, с которыми ему придется иметь дело. Более обстоятельное изложение этих методов будет дано в дальнейшем на конкретных примерах.

В самых простейших случаях задачи на аналитический расчет полей решаются путем использования теоремы Гаусса в интегральной форме (11.13). В более сложных случаях аналитическое решение задач третьей группы производится путем решения уравнения Лапласа.

Аналитические методы решения задач третьей группы могут быть подразделены на две подгруппы. В первой из них производится интегрирование уравнения Лапласа без использования вспомогательных (искусственных) приемов. Во второй подгруппе задача решается путем использования искусственного приема — метода зеркальных изображений. По методу зеркальных изображений решение производится путем введения вспомогательного заряда или зарядов, которые в расчетном отношении заменяют связанные заряды, выявившиеся на границах тел или сред в результате их поляризации или в результате электростатической индукции.

В тех случаях, когда потенциал j является функцией только одной координаты выбранной системы координат, уравнение Лапласа из уравнения в частных производных переходит в обыкновенное дифференциальное уравнение второго порядка, которое интегрируется без затруднений.

Если же потенциал j является функцией двух или трех координат, то для того, чтобы проинтегрировать уравнение Лапласа, в этом случае путем применения метода Фурье — Бернулли следует перейти от уравнения в частных производных к равносильной ему совокупности двух или, соответственно, трех обыкновенных дифференциальных уравнений.

Графический метод анализа и расчета задач третьей группы представляет собой метод, в котором по определенным правилам производится построение семейства силовых и эквипотенциальных линий путем использования некоторых заранее известных свойств исследуемого поля. Эти правила практически одни и те же для всех неизменных во времени полей, т. е. для электростатического поля, электрического поля постоянного тока в проводящей среде (глава 12) и для магнитного поля постоянного тока (глава 13). В силу того, что графический метод решения наиболее часто применяется для анализа магнитных полей, он рассматривается не в данной главе, а в главе магнитное поле постоянного тока.

Анализ и расчет электростатических полей методом моделирования основывается на использовании аналогии между электростатическим полем и электрическим полем постоянного тока в проводящей среде. Метод моделирования основан на том, что каждой задаче электростатики может быть сопоставлена сходная задача на электрическое поле постоянного тока в проводящей среде, в которой совокупность силовых и эквипотенциальных линий практически такая же, что и в электростатической задаче. Это обстоятельство дает возможность перенести результаты экспериментального исследования поля в проводящей среде на род­ственную электростатическую задачу. Следует заметить, что при расчетах полей широко применяется метод наложения.

В заключение отметим, что в задачах электростатики расчет может производиться либо с целью определения «точечной» характеристики поля (напряженности или потенциала в заданной точке), либо с целью определения интегральной характеристики данного поля, например, емкости или разности потенциалов. Перейдем к рассмотрению некоторых простейших электростатических задач.

Поле заряженной оси

Под заряженной осью понимают весьма тонкий теоретически бесконечно длинный металлический проводник (тонкая проволока). Заряд на единицу длины ее принято обозначать t. Электрическая проницаемость среды, окружающей ось, равна e. Для нахождения напряженности поля в некото­рой точке, удаленной на расстоянии r от оси (рис. 11.13), проведем через эту точку цилиндри­ческую поверхность так, что ось цилиндрической поверхности совпадает с заряженной осью. При­меним теорему Гаусса. Элементы ds боковой поверхности и напряженность электрического поля Е в любой точке цилиндрической поверхности по направлению совпадают, потому

, или . (11.39)

Рис. 11.13. Напряженность поля Е заряженной оси.

Напряженность в поле заряженной оси изменяется обратно пропорционально расстоянию r точки от оси. Потенциал

(11.40)

изменяется по логарифмическому закону.