Условия на границе раздела проводящего тела и диэлектрика

На границе проводящее тело — диэлектрик всегда выполняются два условия:

1) отсутствует тангенциальная (касательная к поверхности) составляющая напряженности поля:

E_t=0 (11.34)

2) вектор электрического смещения D в любой точке диэлектрика, непосредственно примыкающей к поверхности проводящего тела, численно равен плотности заряда s на поверхности проводящего тела в этой точке, т. е.

D=s. (11.35)

Рассмотрим первое условие. Все точки поверхности проводящего тела имеют один и тот же потенциал. Следовательно, между двумя любыми весьма близко расположенными друг к другу точками поверхности приращение потенциала dj=0, но dj=E_tdl, следова­тельно, E_tdl=0.

Так как элемент пути dl между точками на поверхности не равен нулю, то равно нулю E_t.

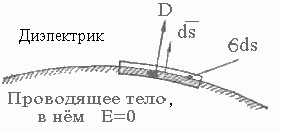Рис. 11.10. Условия на границе раздела двух тел.

Для доказательства второго условия мысленно выделим бесконечно малый параллелепипед (рис. 11.10). Верхняя грань его параллельна поверхности проводящего тела и расположена в диэлектрике. Нижняя грань находится в проводящем теле. Высоту параллелепипеда возьмем весьма малой (сплющим его). Применим к параллелепипеду тео­рему Гаусса. В силу малости линейных размеров можно принять, что плотность заряда s на поверхности ds проводящего тела, попавшей внутрь параллелепипеда, одна и та же. Полный заряд внутри рассматриваемого объема равен sds.

Поток вектора D через верхнюю грань объема равен Dds=Dds. Потока вектора D через боковые грани объема в силу малости последнего и в силу того, что вектор D скользит по ним, нет. Через «дно» объема поток также отсутствует, так как внутри проводящего тела E=0 и D=0 (e проводящего тела есть величина конечная). Таким образом, поток вектора D из объема равен Dds=sds или D=0.