Обобщенные координаты, скорости, ускорения. Обобщенные силы. Определение числа степеней свободы систем тел

Любые независимые параметры определяющие положение точек или тел системы в пространстве называются обобщенными координатами и обозначаются (q_1,q₂,…,q_n).

Обобщенная скорость равна первой производной от обобщенной координаты по времени, обобщенное ускорение – 2-й производной от обобщенной коодинаты по времени.

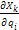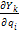Q_i=∑(F_kx +F_ky +F_kz 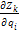) – обобщенная сила

Если на систему действуют только потенциальные силы то Q_i=-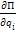

Свободная система n материальных точек имеет 3n степеней свободы, у несвободной меньше 3n.

Уравнение Лагранжа 2-го рода.

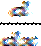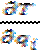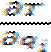()- =Q_i - Уравнение Лагранжа 2-го рода

Число уравнений Лагранжа равно числу обобщенных координат(числу степеней свободы)

Уравнение Лагранжа 2-го рода для консервативных систем. Кинетический потенциал.

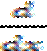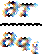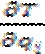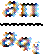()- = - Уравнение Лагранжа 2-го рода для консервативных систем

Функция L=T-П – кинетический потенциал.